L'énoncé
Cet exercice est un QCM. Coche la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
On considère la figure ci-dessous :
Ce cercle est circonscrit au triangle \(ABC\), il a pour centre le point \(O\) et le point \(M\) est un point de ce cercle.
\(ABC\) est un triangle isocèle en \(A\) tel que \(\widehat{ABC} = 75°\).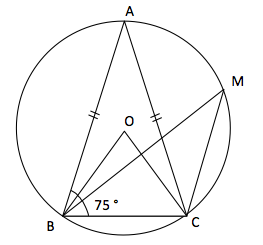
Combien mesure l'angle \(\widehat{ACB} \) ?
\(\widehat{ACB}= 75° \)
\(\widehat{ACB}= 105° \)
\(\widehat{ACB}= 90° \)
Aucune des réponses précédentes n’est exacte.
Dans un triangle isocèle, les angles à la base sont égaux.
Question 2
On considère la figure ci-dessous :
Ce cercle est circonscrit au triangle \(ABC\), il a pour centre le point \(O\) et le point \(M\) est un point de ce cercle.
\(ABC\) est un triangle isocèle en \(A\) tel que \(\widehat{ABC} = 75°\).
\(\widehat{ACB} = 75°\)
Combien mesure l'angle \(\widehat{BAC} \) ?
\(\widehat{BAC} = 75° \)
\(\widehat{BAC} = 105° \)
\(\widehat{BAC} = 30° \)
Aucune des réponses précédentes n’est exacte.
Dans un triangle, la somme des angles est égale à 180°.
Question 3
On considère la figure ci-dessous :
Ce cercle est circonscrit au triangle \(ABC\), il a pour centre le point \(O\) et le point \(M\) est un point de ce cercle.
\(ABC\) est un triangle isocèle en \(A\) tel que \(\widehat{ABC} = 75°\).
\(\widehat{BAC} = 30°\)
Combien mesure l'angle \(\widehat{BMC} \) ?
\(\widehat{BMC} = 75°\)
\(\widehat{BMC} = 90°\)
\(\widehat{BMC} = 30°\)
Aucune des réponses précédentes n’est exacte.
Nous y voilà ! Il faut maintenant utiliser la règle des « angles inscrits ».
Dans un cercle, deux angles inscrits qui interceptent le même arc sont égaux.
Question 4
On considère la figure ci-dessous :
Ce cercle est circonscrit au triangle \(ABC\), il a pour centre le point \(O\) et le point \(M\) est un point de ce cercle.
\(ABC\) est un triangle isocèle en \(A\) tel que \(\widehat{ABC} = 75°\).
\(\widehat{BAC} = 30°\) et \(\widehat{BMC} = 30°\)
Combien mesure l'angle \(\widehat{BOC} \) ?
\(\widehat{BOC} = 30°\)
\(\widehat{BOC} = 60°\)
\(\widehat{BOC} = 15°\)
Aucune des réponses précédentes n’est exacte.
Et nous y voilà encore! Il faut maintenant utiliser la règle de « l’angle au centre ».
Dans un cercle, un angle inscrit est égal à la moitié de l’angle au centre qui intercepte le même arc.
Question 5
On considère la figure ci-dessous :
Ce cercle est circonscrit au triangle \(ABC\), il a pour centre le point \(O\) et le point \(M\) est un point de ce cercle.
\(ABC\) est un triangle isocèle en \(A\) tel que \(\widehat{ABC} = 75°\).
Petit exercice intellectuel :
Imagine que tu construis le point \(P\) diamétralement opposé au point \(C\).
Combien mesure l'angle \(\widehat{BPO} \) ?
\(\widehat{BPO} = 30° \)
\(\widehat{BPO} = 60° \)
\(\widehat{BPO} = 75° \)
Aucune des réponses précédentes n’est exacte.
Attention : petit piège ! \( \widehat{BPO}\) est-il un angle inscrit ?
Bien sûr ! \( \widehat{BPO} = \widehat{BPC}\) ! C’est le même angle !
Dans un cercle, deux angles inscrits qui interceptent le même arc sont égaux.
\( \widehat{BPC}, \widehat{BAC},\) et \( \widehat{BMC}\) interceptent le même arc.
Question 6
On considère la figure ci-dessous :
Ce cercle est circonscrit au triangle \(ABC\), il a pour centre le point \(O\) et le point \(M\) est un point de ce cercle.
\(ABC\) est un triangle isocèle en \(A\) tel que \(\widehat{ABC} = 75°\).
Pour terminer avec cet exercice, combien mesure l'angle \(\widehat{PBC} \) ?
\(\widehat{PBC} = 75° \)
\(\widehat{PBC} = 60° \)
\(\widehat{PBC} = 90° \)
Aucune des réponses précédentes n’est exacte.
Attention : petit piège ! Ici, plus rien à voir avec les angles inscrits ou les angles au centre.
Regarde bien le triangle \(BPC\).
Quelle place occupe le côté \([PC]\) pour le cercle ?
C’est un diamètre du cercle.
Si un triangle est inscrit dans un cercle et a pour côté un diamètre de ce cercle alors il est rectangle.
Question 7
On considère la figure ci-dessous :
Ce cercle est circonscrit aux triangles \(BFD\) et \(CBD\),
\( \widehat{BFD} = 60°\) et \(\widehat{BDC} = 20°\)
On veut savoir combien mesure l'angle \(\widehat{CBD} \).
Mais avant cela on va dabord calculer l'angle \(\widehat{BCD} \).
Combien mesure l'angle \(\widehat{BCD} \) ? 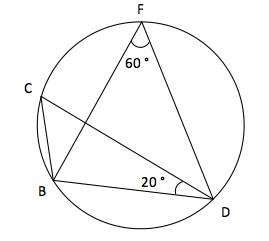
\(\widehat{BCD} = 80° \)
\(\widehat{BCD} = 60° \)
\(\widehat{BCD} = 20° \)
Aucune des réponses précédentes n’est exacte.
Il faut maintenant utiliser la règle des « angles inscrits ».
Dans un cercle, deux angles inscrits qui interceptent le même arc sont égaux.
\(\widehat{BCD}\)et \(\widehat{BFD}\) interceptent le même arc.
Question 8
On considère la figure ci-dessous :
Ce cercle est circonscrit aux triangles \(BFD\) et \(CBD\),
\( \widehat{BFD} = 60°\) et \(\widehat{BDC} = 20°\) 
\(\widehat{BCD} = 60° \)
Combien mesure l'angle \(\widehat{CBD} \)?
\(\widehat{CBD} = 100° \)
\(\widehat{CBD} = 80° \)
\(\widehat{CBD} = 20° \)
Aucune des réponses précédentes n’est exacte.
Dans un triangle, la somme des angles est égale à 180 °.
Place-toi dans le triangle \(BCD\).
Question 9
Voici un hexagone régulier de centre \(O\).
Quelle est la nature des triangles \(ABO, BCO, CDO, DEO, EFO\) et \(FAO\) ?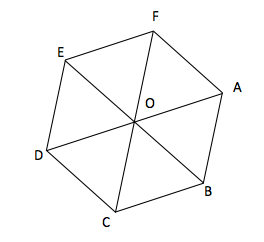
Ce sont des triangles quelconques.
Ce sont des triangles isocèles.
Ce sont des triangles équilatéraux.
Ce sont des triangles rectangles.
\(ABCDEF\) est un hexagone régulier, donc les « angles au centre » sont égaux et mesure \(\frac{360}{6}\), c’est-à-dire 60°.
Les longueurs \(OA, OB, OC, OD, OE\) et \( OF\) sont égales (ce sont des rayons du cercle).
Donc les triangles \(ABO, BCO, CDO, DEO, EFO\) et \(FAO\) ont (au moins) deux côtés égaux.
Dans chaque triangle, les trois angles sont donc égaux à 60°, donc ce sont des triangles …
Question 10
Quelle doivent être les caractéristiques d'un polygone pour qu'il soit « régulier » ?
Il doit avoir tous ses côtés de même longueur.
Il doit avoir des angles de même mesure.
Il doit avoir tous ses côtés de même longueur et ses angles de même mesure.
Il doit avoir des diagonales de même longueur.
Triangle équilatéral, carré, pentagone régulier, hexagone régulier …
Un losange a ses côtés de même longueur, cela suffit-il à en faire un polygone régulier ?
