Fiche de cours
Définition de l'intégrale
Définition
Soit (O,$\overrightarrow {i}$,$\overrightarrow {j}$) un repère orthonormé et une fonction $f$ continue et positive sur un intervalle $[a,b]$.
$\mathcal{D}$ est le domaine du plan délimité par $x$=$a$ , $x$=$b$, l'axe des abscisses et $\mathcal{C}_f$, la courbe représentative de la fonction $f$.
L'intégrale de $f$ sur $[a,b]$ notée $ \displaystyle \int \limits_a^b f (t)dt$ est l'aire $\mathcal{A}$ du domaine $\mathcal{D}$ exprimée en unités d'aire.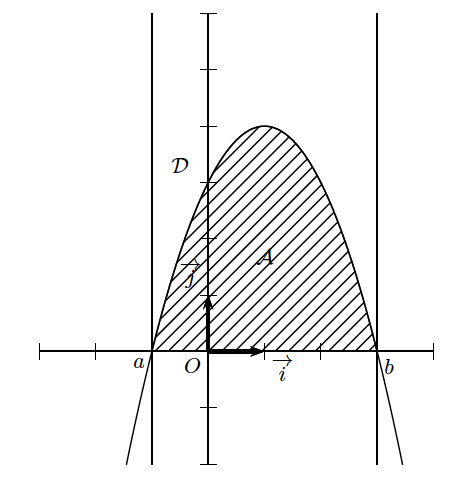
Exemple
Calculer $I = \displaystyle \int_{1}^4 x dx = \int_{1}^4 t dt$ ($x$ et $t$ sont des variables muettes).
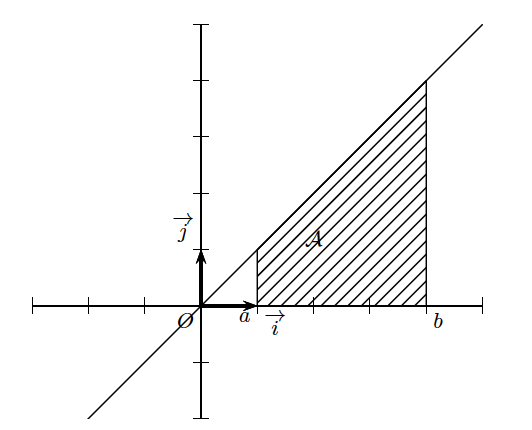
Etape 1 : On repère l'aire recherchée.
Etape 2 : On remarque qu'il s'agit d'un trapèze rectangle.
Etape 3 : La formule du calcul d'aire du trapèze rectangle est connue. On peut l'utiliser pour calculer l'intégrale :
$ A = \dfrac{(B + b) \times h}{2}$
$ A = \dfrac{5 \times 3}{2}$
Finalement, $I = \dfrac
