1
Video
Étude de la fonction cosinus
2
Video
Propriétés de la fonction cosinus
3
Video
Étude de la fonction sinus
4
Video
Propriétés de la fonction sinus
5
Exercice
Exercice - Trigonométrie et calculs élémentaires
6
Video
Équations trigonométriques
7
Exercice
Exercice - Équations trigonométriques
8
Video
Calculs de limites de fonctions trigonométriques
9
Video
Dérivation des fonctions trigonométriques
10
Exercice
Exercice - Étude d'une fonction trigonométrique - bac
Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Equations trigonométriques
Egalité de cosinus ou de sinus
Conditions d'égalité de deux cosinus :
$ \cos(x)=\cos(a) \Leftrightarrow x=a+2k\pi \text{ ou } x=-a+2k\pi \text{ avec } k\in \mathbb{Z}$
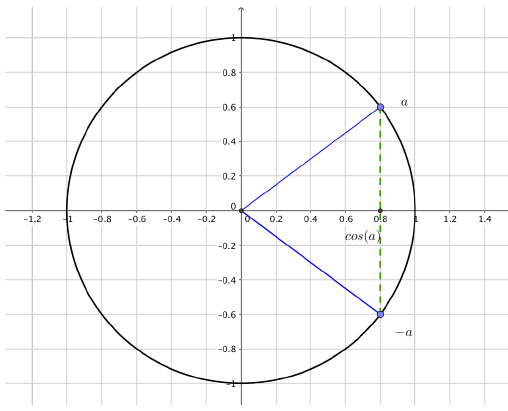
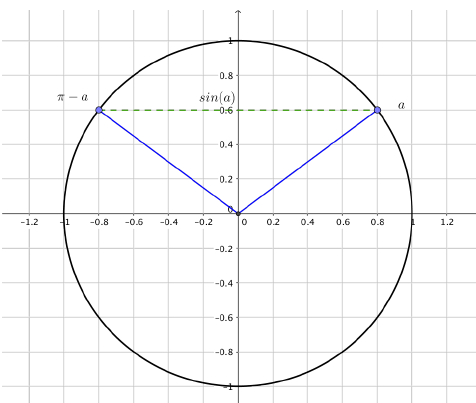
Conditions d'égalité de deux sinus :
$\sin(x)=\sin(a) \Leftrightarrow x=a+2k\pi \text{ ou } x=(\pi-a)+2k\pi \text{ avec } k\in\mathbb{Z}$
Exemple
Résoudre dans $\mathbb{R}$ l'équation $\sin(3x)=\dfrac{\sqrt2}{2}$
On a $\dfrac{\sqrt2}{2}=\sin\left( \dfrac{\pi}{4}\right)$ d'après le cours, donc :
$\sin(3x)=\dfrac{\sqrt2}{2} \Leftrightarrow 3x=\dfrac{\pi}{4}+2k\pi$ ou $3x=\left(\pi-\dfrac{\pi}{4}\right)+2k\pi = \dfrac{3\pi}{4}+2k\pi $
C'est à dire :
$x=\dfrac{\pi}{12}+\dfrac{2k\pi}{3}$ ou $x=\dfrac{\pi}{4}+\dfrac{2k\pi}{3}$ avec $k\in\mathbb{Z}$
