L'énoncé
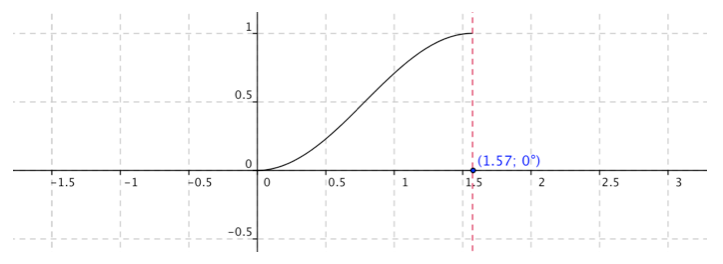
Dans tout cet exercice, on considère la fonction \(f\) définie sur \(\mathbb{R}\) par : \(f(t) = \sin^2(t)\). On note \(C_f\) sa courbe représentative.
Question 1
Partie A : étude de la fonction \(f\).
Justifier que la fonction \(f\) est périodique de période \(\pi\).
En déduire que l'on peut mener l'étude de \(f\) sur l'intervalle \(\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\).
On a :
\(f(t+\pi) = \sin^2(t+\pi)\)
\(f(t+\pi)=(\sin(t+\pi))^2\)
\(f(t+\pi)=(-\sin(t))^2\)
\(f(t+\pi)=\sin^2(t)\)
\(f(t+\pi)=f(t)\)
Donc \(f\) est bien périodique de période \(\pi\).
De plus lorsque l'on a une fonction périodique de période T, on peut restreindre l'étude de cette fonction à n'importe quel intervalle de longueur T : ici, on fait donc l'étude sur un intervalle de longueur \(\pi\) : l'intervalle proposé convient puisqu'il s'agit de \(\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\) (et qu'il est bien de longueur \(\pi\)).
Evidemment, il faut connaître par cœur la définition de « fonction périodique »
On a besoin d’exprimer \(f(t+\pi).\)
N’oubliez pas que \(\sin(t+\pi) = -\sin(t)\)
Question 2
La fonction \(f\) est-elle paire, impaire ? Justifier la réponse.
\(f\)est définie sur \(\mathbb{R}\). Cherchons une relation entre \(f(t)\) et \(f(-t)\).
\(f(-t) = \sin^2(-t) = (\sin(-t))^2 = \sin^2(t)=f(t)\)
On en déduit que \(f\) est paire et que l'axe des ordonnées est un axe de symétrie pour la courbe représentative de \(f\).
On écrit la formule de \(f(-t)\) !
\(\sin(-t)\) est égal à ? (Utilise le cercle trigonométrique !)
On a \(\sin(-t) = -\sin(t)\) : et en plus de tout ça, on a des carrés !
Question 3
À quel intervalle peut-on alors restreindre l'étude la fonction \(f\) ?
La fonction \(f\) est paire donc l'axe des ordonnées est un axe de symétrie pour la courbe de \(f\).
On peut donc limiter l'étude de \(f\) aux réels \(t\) positifs. Mais comme on faisait déjà juste l'étude sur \(\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\) on peut ici se limiter à : \(I =\left[0;\dfrac{\pi}{2}\right]\)
Que se passe-t-il pour le graphique lorsque la fonction est paire ?
Question 4
Justifier que \(f\) est dérivable sur \(\mathbb{R}\) et calculer \(f'(t)\).
On pose : \(u(t) = \sin(t)\)
La fonction \(u\) est dérivable sur \(\mathbb{R}\).
On a : \(u'(t) = \cos(t)\)
Comme \((u^2)' = 2 \times u' \times u\)
C'est la formule \((u^n)' = n \times u' \times u^{n-1}\) où \(n=2\)
\(f'(t) = 2\cos(t) \times \sin(t)\)
On utilise ici la formule sur la dérivation de \(u^2\)
La formule est : \((u^2)' = 2 \times u' \times u\) avec \(u(t) = \sin(t)\)
Question 5
Etudier le signe de \(f'(t)\) sur l'intervalle \(\left[0;\dfrac{\pi}{2}\right]\).
On sait que : \(f'(t) = 2 \cos(t) \times \sin(t)\)
On cherche la ou les valeurs où la dérivée s'annule :
On a \(f'(t) = 0 \Leftrightarrow \sin(t)=0\) ou \(\cos(t)=0\)
Sur \(\left[0;\dfrac{\pi}{2}\right]\),
\(\sin(t)\) s'annule uniquement pour \(t = 0\),
\(\cos(t)\) s'annule uniquement pour \(t = \dfrac{\pi}{2}\).
On cherche le signe de la dérivée : Le signe de \(f'(t)\) dépend uniquement du signe sur l'intervalle \(\left[0;\dfrac{\pi}{2}\right]\) de \(\cos(t)\) et de celui de \(\sin(t)\).
On lit les signes sur le cercle trigonométriques : entre \(0\) et \(\dfrac{\pi}{2}\), on voit que \(\cos(t)\) et \(\sin(t)\) sont tous les deux positifs. Leur produit l'est aussi.
On peut résumer tout cela dans le tableau de signes :
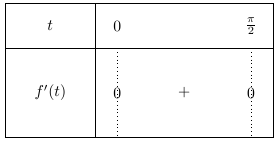
On cherche déjà quand la dérivée s’annule, et surtout faites bien attention, on ne fait l’étude que sur \(\left[0;\dfrac{\pi}{2}\right]\).
Pour les signes, c’est toujours pareil : faire la lecture sur le cercle trigonométrique ! Et encore une fois, c’est plus facile ici car l’on se place sur \(\left[0;\dfrac{\pi}{2}\right]\).
Question 6
En déduire le tableau de variations de \(f\) sur \(\left[0;\dfrac{\pi}{2}\right]\).
D'après les résultats précédents, \(f\) est croissante sur\(\left[0;\dfrac{\pi}{2}\right]\)
On a aussi :
\(f(0) = \sin^2(0) = 0\)
\(f\left(\dfrac{\pi}{2}\right) = \sin^2(\frac{\pi}{2})=1\)
On a finalement le tableau de variations suivant :
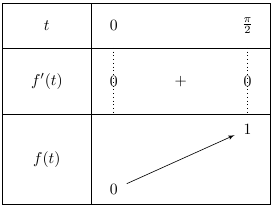
N’oubliez pas de calculer les images de $0$ et de \(\dfrac{\pi}{2}\).
Question 7
Partie B : construction de la courbe représentative.
Dans toute cette question, on s'intéresse à la construction de la courbe de \(f\) :
Compléter le tableau de valeurs suivant :
| $t$ | $0$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ |
| $f(t)=\sin^2(t)$ |
| $t$ | $0$ | $\dfrac{\pi}{6}$ | $\dfrac{\pi}{4}$ | $\dfrac{\pi}{3}$ | $\dfrac{\pi}{2}$ |
| $f(t)=\sin^2(t)$ | $0$ | $\dfrac{1}{4}$ | $\dfrac{1}{2}$ | $\dfrac{3}{4}$ | $1$ |
Vous pouvez ici utiliser le formulaire (pour les valeurs usuelles) ou votre calculatrice (si elle est en mode radian).
Question 9
En utilisant les propriétés de la courbe vues aux questions 1 et 2, construire en justifiant la courbe de \(f\) sur \(\mathbb{R}\)
Maintenant que l'on a la courbe sur \(\left[0;\dfrac{\pi}{2}\right]\), on obtient d'abord la courbe sur \(\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\) en utilisant la symétrie par rapport à l'axe des ordonnées :
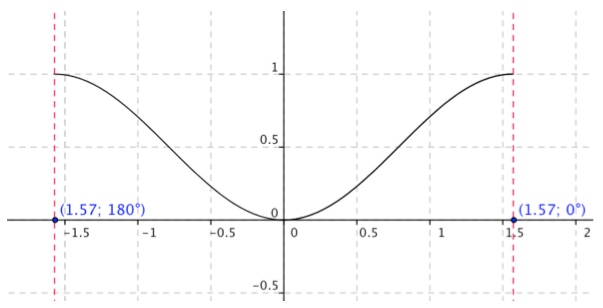
Enfin, on obtient toute la courbe en utilisant la périodicité : il suffît de reprendre le motif obtenu, et de la translater vers la droite et vers la gauche de \(k\pi\) unités (puisque c'est la période).
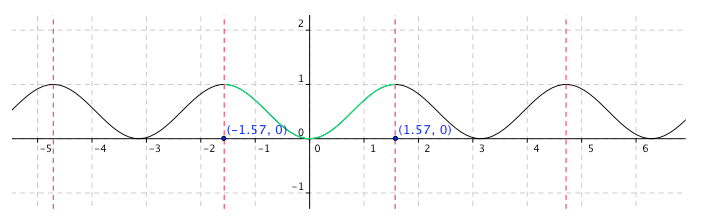
Pensez à la parité de \(f\) : c’est maintenant qu’elle est utile !
Il y a aussi la périodicité : le même schéma de courbe va se répéter !
Question 10
Partie C : Un calcul d'aire.
Restitution organisée de connaissances :
On admet dans cette question que, quelque soit le réel \(t\) on a : \(\cos(2t)=\cos^2(t)-\sin^2(t)\)
Démontrer alors que pour tout réel \(t\), on a \(\cos(2t)=1-2\sin^2(t)\)
On sait que l'on a pour tout réel $t$ : : \(\cos^2(t)+\sin^2(t)=1\) (Et oui, en voilà une qui sert souvent !)
Soit : \(\cos^2(t)=1-\sin^2(t)\)
Donc comme \(\cos(2t) = \cos^2(t)-\sin^2(t)\)
On en déduit que : \(\cos(2t)=(1-\sin^2(t))-\sin^2(t)\)
\(\cos(2t)=1-2\sin^2(t)\)
Pour tout réel $a$, on a : \(\cos^2(a)+\sin^2(a)=1\)
On isole $\cos^2(a)$
On remplace dans l'égalité
Question 11
En déduire \(\sin^2(t)\) en fonction de \(\cos(2t)\).
Comme on a \(\cos(2t) = 1 - 2\sin^2(t)\), on en déduit :
\(2\sin^2(t)=1-\cos(2t)\)
\(\sin^2(t) = \dfrac{1-\cos(2t)}{2}\)
Question 12
En déduire la valeur de l'intégrale \(I= \displaystyle\int_{0}^{\pi} f(t)dt\)
\(I= \displaystyle\int_{0}^{\pi} f(t)dt = \displaystyle\int_{0}^{\pi} \sin^2(t)dt\)
\(I= \displaystyle\int_{0}^{\pi} \dfrac{1-\cos(2t)}{2}dt\)
\(I=\displaystyle\int_{0}^{\pi}\dfrac{1}{2}dt-\displaystyle\int_{0}^{\pi}\dfrac{\cos(2t)}{2}dt\)
\(I=\left[\dfrac{t}{2}\right]^{t=\pi}_{t=0} - \dfrac{1}{2}\displaystyle\int_{0}^{\pi}\cos(2t)dt\)
\(I=\dfrac{\pi}{2}-0- \dfrac{1}{2}\left[\dfrac{\sin(2t)}{2}\right]^\pi_0\)
\(I=\dfrac{\pi}{2}-\dfrac{1}{2}\left( \dfrac{\sin(2\pi)}{2}-\dfrac{\sin(0)}{2}\right)\)
\(I=\dfrac{\pi}{2}-\dfrac{1}{2}(0-0)\)
\(I=\dfrac{\pi}{2}\)
Déjà il faut remplacer par \(\sin^2(t) = \dfrac{1-cos2t}{2}\) et ensuite couper l’intégrale en deux morceaux plus « faciles ».
Une primitive de \(\cos(2t)\) est \(\dfrac{\sin(2t)}{2}\)
Question 13
Déterminer l'aire $A$, en cm\(^2\), du domaine délimité par la courbe, l'axe des abscisses, et les droites d'équation \(x = 0\) et \(x=\pi\).
L'aire demandée est égale à $I$ en unité d'aire.
Donc : \(A = \dfrac{\pi}{2}u.a\)
Pensez aux intégrales.
Une intégrale d'une fonction positive est une aire