$(C)$ est le cercle de diamètre $[RM]$ avec $RM = 10$ cm.
Soit $T$ un point de $(C)$ tel que $RT = 6$ cm.
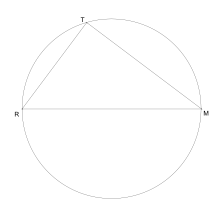
1) Faire une figure à l'échelle.
2) Démontrer que le triangle $RTM$ est rectangle.
3) Montrer que $TM = 8$ cm.
4) $S$ est un point de la demi-droite $[TM)$ tel que $TS = 10$ cm.
La droite perpendiculaire à $(TM)$ passant par $S$ coupe $(RM)$ en $H$.
A) Compléter la figure de la question 1)
B) Démontrer que les droites $(SH)$ et $(RT)$ sont parallèles.
C) Calculer $SH$
1)
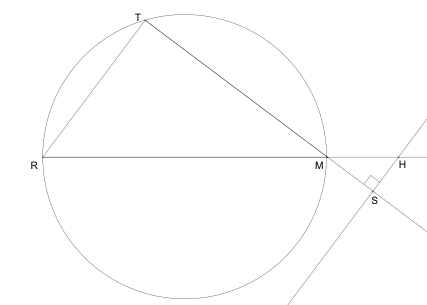
2) Le triangle $RTM$ est inscrit dans le cercle de diamètre $[RM]$ donc il est rectangle en $T$.
3) On applique le théorème de Pythagore dans le triangle $RTM$ rectangle en $T$ :
$RM^2 = RT^2 + TM^2$ soit $10^2 = 6^2 + TM^2$
$TM^2 = 100 - 36 = 64$
Donc $TM = \sqrt{64}$ soit $TM = 8$ cm.
4) A) Les droites $(RT)$ et $(SH)$ sont toutes deux perpendiculaires à la droite $(TM)$ donc elles sont parallèles.
B) On considère les triangles $MHS$ et $MTR$, on a :
$R \in (MH)$, $T \in (MS)$ et $(RT) \ // \ (SH)$
D'après le théorème de thalès, on peut écrire : $\dfrac{MR}{MH} = \dfrac{MT}{MS} = \dfrac{RT}{SH}$ soit $\dfrac{10}{MH} = \dfrac{8}{2} = \dfrac{6}{SH}$
$SH = \dfrac{6\times 2}{8}$ soit $SH = 1,5$ cm.
