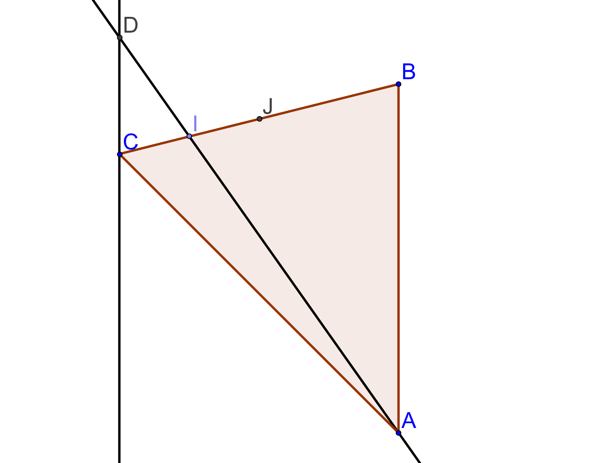
L'énoncé
On considère un triangle \(ABC\) tel que :
- \(I\) est le point du segment \([BC]\) tel que l’on ait \(BI = \dfrac{3}{4} BC\).
- \(J\) est le milieu du segment \([BC]\).
- \((\Delta)\) soit la droite parallèle à \((AB)\) passant par \(C\).
- \(D\) soit le point d’intersection de \((AI)\) et de \((\Delta)\).
Question 1
Faites une figure soignée.
Question 2
Déterminez la valeur exacte du rapport \(\dfrac{IB}{IC}\).
Le point \(I\) est un point du segment \([BC]\) donc :
\(IC = BC - \dfrac{3}{4} BC\)
\(IC = \dfrac{1}{4} BC \)
Ainsi : \(\dfrac{IB}{IC} = \dfrac{\dfrac{3}{4} BC}{\dfrac{1}{4} BC} = 3\)
Conclusion : \(\dfrac{IB}{IC} = 3\)
On sait que \(BI = \dfrac{3}{4} BC\).
Exprimez à présent \(IC\) en fonction de \(BC\).
Calculez alors le rapport demandé.
Question 3
Déduisez de la première question en utilisant le théorème de Thalès que \(AB = 3CD\).
Dans le triangle \(BIA\), on a : \(D\) appartient à \((IA)\).
\(C\) appartient à \((BI)\).
\((BA) // (CD)\).
D'après le théorème de Thalès, on a : \(\dfrac{IB}{IC} = \dfrac{IA}{ID} = \dfrac{BA}{CD}\)
On sait de plus que \(\dfrac{IB}{IC} = 3\)
Ainsi : \(\dfrac{BA}{CD} =3\)
Conclusion : \(BA = 3CD\)
Il faut utiliser la propriété de Thalès dans la configuration « du papillon ». Voyez-vous les deux droites parallèles ?
\((AB) // (CD)\)
Question 4
Construisez sur la figure la médiane issue de \(A\) du triangle \(ABC\). Celle-ci coupe \((\Delta)\) en \(E\). Quelle est alors la nature du quadrilatère \(ABEC\) ? Justifier votre réponse.
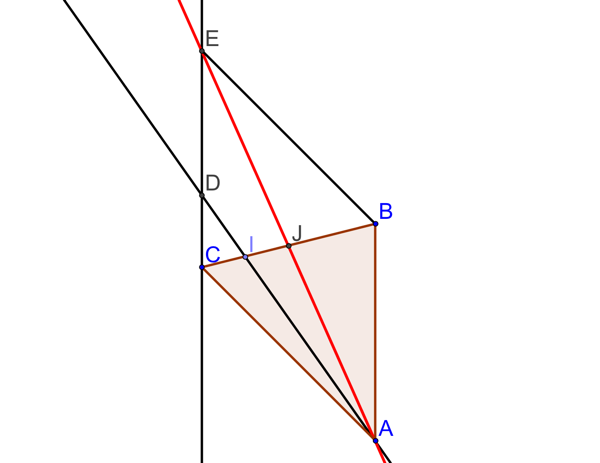
On considère la symétrie \(S\) de centre \(J\).
\(S(B) = C\) car \(J\) est le milieu de \([BC]\).
Notons \(S(A) = A\) et montrons que \(A = E\).
\(S(B) = C\)
\(S(A) = A\) donc les points \(A\), \(A\) et \(J\) sont alignés.
\(S((AB)) = (CA)\). L'image dune droite par une symétrie centrale est une droite parallèle donc les droites \((AB)\) et \((CA)\) sont parallèles. Le point \(A\) appartient donc à la parallèle à \((AB)\) passant par \(C\) : c'est la droite \((\Delta)\).
Finalement, le point \(A\) appartient à la fois à \((AJ)\) et à \((\Delta)\). D'après l'énoncé, \(A\) est confondu avec \(E\).
Conclusion \(A = E\) et les diagonales de \(ABEC\) ont le même milieu donc c'est un parallélogramme.
Réfléchissez aux diagonales du quadrilatère.
On sait déjà que \(J\) est le milieu de \([BC]\).
On sait aussi que \((BA)\) et \((CE)\) sont parallèles. Vous pouvez utiliser une symétrie et conclure.
Question 5
Supposons à présent que \(BAC\) ait été isocèle en \(A\). Quelle aurait été la nature de \(ABEC\) ?
\(BA = AC\) donc \(ABEC\) est un parallélogramme ayant deux côtés consécutifs de même longueur.
On en déduit donc que \(ABEC\) serait dans ce cas un losange.
Avec une contrainte en plus, la nature de \(ABEC\) reste au minimum un parallélogramme.
A-t-il de nouvelles propriétés ?