L'énoncé
Cocher la bonne réponse
Tu as obtenu le score de
Question 1
Soit $ABC$ un triangle et $D$ et $E$ deux points des droites $(AB)$ et $(AC)$ tels que les droites $(BC)$ et $(DE)$ sont parallèles,
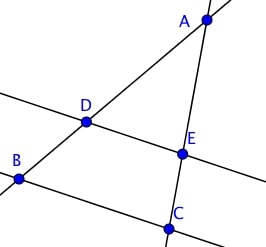
D'après le théorème de Thales, quelles égalités peut-on écrire ?
$\dfrac{AD}{AB} = \dfrac{AE}{AC}=\dfrac{DE}{BC}$
$\dfrac{AD}{AB} = \dfrac{AE}{AC}=\dfrac{BC}{DE}$
$\dfrac{AD}{AB} = \dfrac{AC}{AE}=\dfrac{DE}{BC}$
Question 2
Que permet de démontrer la réciproque du théorème de Thalès ?
Qu'un triangle est rectangle.
Que deux droites dans un triangle sont parallèles.
Il faut vérifier que certaines égalités sont vérifiées et cela permet de conclure sur le parallélisme de deux droites.
Que deux droites dans un triangle ne sont pas parallèles.
Question 3
Quelle hypothèse fondamentale doit on vérifier pour appliquer le théorème de Thalès ?
Que la valeur en bourse de Thalès est plus grande que celle de Safran.
Que les égalités sont vérifiées.
Que les droites sont parallèles.
En effet, si l'énoncé ne l'indique pas ou si le parallélisme n'a pas été prouvé auparavant, il n'est pas possible d'appliquer le théorème.
Question 4
Les droites $(DE)$ et $(BC)$ sont parallèles,
Que vaut $AC$ ?
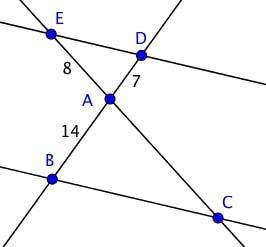
$4$
$14$
$16$
En effet, d'après le théorème de Thalès appliqué aux triangles $AED$ et $ABC$, on a $\dfrac{AE}{AC}= \dfrac{AD}{AB}$ c'est à dire $\dfrac{7}{14} = \dfrac{8}{AB}$ donc $AB = 2 \times 8 = 16$
Question 5
Comment savoir si les droites $(DE)$ et $(BC)$ sont parallèles ?
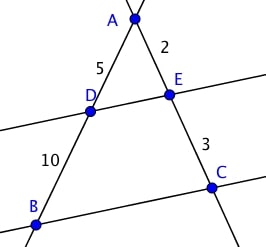
Avec un règle, en mesurant l'écart entre les deux droites !
On voit très bien que les droites sont parallèles sur la figure !
Avec le théorème de Thalès
Avec le réciproque du théorème de Thalès
On commence par calculer les rapports et en fonction de leur égalité ou non, on conclue.
Question 6
Les droites $(DE)$ et $(BC)$ sont-elles parallèles ?
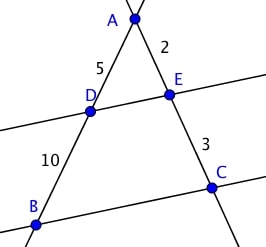
Oui
Non
En effet, calculons séparément $\dfrac{AD}{AB}$ et $\dfrac{AE}{AC}$ :
$\dfrac{AD}{AB} = \dfrac{5}{10+5} = \dfrac{5}{15} = \dfrac{1}{3}$
$\dfrac{AE}{AC} = \dfrac{2}{2 + 3} = \dfrac{2}{5}$
Or $\dfrac{1}{3} \neq \dfrac{2}{5}$, d'après la contraposé du théorème de Thalès, les droites $(DE)$ et $(BC)$ ne sont pas parallèles.
Question 7
$\dfrac{3}{AB} =\dfrac{8}{9}$
Que vaut $AB$ ?
$AB=\dfrac{27}{8}$
$\dfrac{3}{AB} =\dfrac{8}{9}$
On effectue un produit en croix.
$8AB=9\times3$
$AB=\dfrac{27}{8}$
$AB=\dfrac{8}{27}$
$AB=\dfrac{9}{24}$
Question 8

Comment démontrer que les droites $(ED)$ et $(BC)$ sont parallèles ?
Avec une équerre
Avec le théorème de Thalès
A l'aide d'une propriété géométrique
En effet, si deux droites sont perpendiculaires à une même droite alors elles sont parallèles.
Question 9
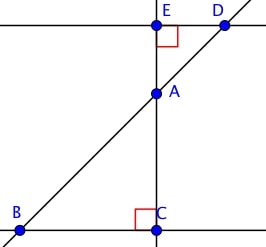
On sait que $(BC) // (ED)$, quelle égalité peut on écrire ?
$\dfrac{EA}{EC} = \dfrac{DA}{DB}$
$\dfrac{DA}{BA} = \dfrac{EA}{CA}$
C'est en effet les égalités du théorème !
$\dfrac{AD}{AC} = \dfrac{AE}{AB}$
Question 10
On sait que $\dfrac{3}{BC} = \dfrac{5}{4}$, que vaut $BC$ ?
$\dfrac{15}{4}$
$\dfrac{3}{20}$
$\dfrac{12}{5}$
En effet, on sait que $\dfrac{3}{BC} = \dfrac{5}{4}$ c'est à dire $3 \times \dfrac{4}{5} = BC$ soit encore $BC = \dfrac{12}{5} = 2,4$

C'est en effet les égalités du théorème.