L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte. (ou incorrecte en fin de QCM)
Tu as obtenu le score de
Question 1
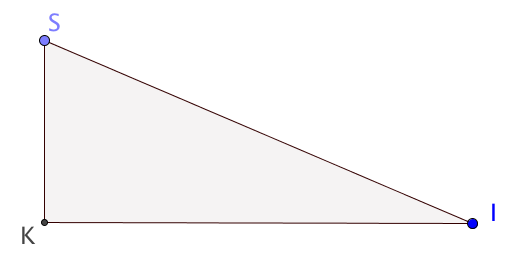
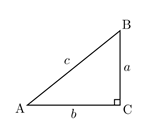
Dans un triangle \(SKI\), rectangle en \(K\), la propriété de Pythagore est :
\(SK^2+KI^2= IS^2\)
\(IK^2+KI^2= IS^2\)
\(SK^2+SI^2= IK^2\)
Aucune des trois réponses précédentes n’est exacte.
Faites une figure.
Besoin d’un rappel ? Allez voir la vidéo dans les prérequis.
Question 2
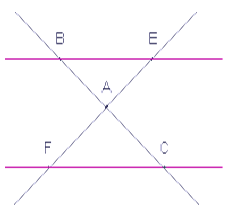
On se place dans la configuration suivante.
\(B\) appartient à \((AC)\),
\(E\) appartient à \((AF)\),
\((BE) // (CF)\).
Appliquez la propriété de Thalès.
\(\dfrac{AC}{AB} = \dfrac{AE}{AF}= \dfrac{BE}{CF}\)
\(\dfrac{AC}{CB} = \dfrac{AE}{EF}= \dfrac{BE}{CF}\)
\(\dfrac{AB}{AC} = \dfrac{AE}{AF}= \dfrac{BE}{CF}\)
Aucune des trois réponses précédentes n’est exacte.
C’est du cours. Il faut le connaître par cœur.
Question 3
Soit \(ABC\) le triangle rectangle en \(C\) ci-dessus. Cochez la bonne réponse.
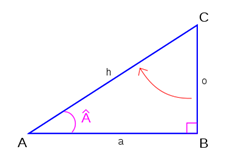
\(sin(Â) = \dfrac{b}{c}\)
\(cos(Â) = 1- sin(Â)\)
\(tan (Â) = \dfrac{a}{b}\)
Aucune des trois réponses précédentes n’est exacte.
C’est du cours. Il faut connaître tout ceci par cœur. Allez revoir la vidéo dans les prérequis.
Question 4
On se place dans la configuration suivante.
\(B\) appartient à \((AC)\),
\(E\) appartient à \((AF)\),
\((BE) // (CF)\).
Appliquez la propriété de Thalès.
\(\dfrac{AC}{AB} = \dfrac{AE}{AF}= \dfrac{BE}{CF}\)
\(\dfrac{AC}{CB} = \dfrac{AE}{EF}= \dfrac{BE}{CF}\)
\(\dfrac{AB}{AC} = \dfrac{AE}{AF}= \dfrac{BE}{CF}\)
Aucune des trois réponses précédentes n’est exacte.
C’est exactement la même configuration que celle vue en question 2.
Les résultats ne devraient pas trop changer.
Question 5
En utilisant la figure ci-dessus, cochez la bonne réponse.
\(BC^2-BA^2=AC^2\)
\(BC^2+BA^2=AC^2\)
\(CB^2-AB^2=AC^2\)
Aucune des trois réponses précédentes n’est exacte.
Il faut utiliser la propriété de Pythagore bien sûr.
Question 6
Soit \(M\) un point de la médiatrice dun segment \([AB]\), cochez la bonne réponse.
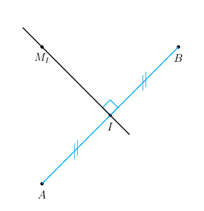
Tous les points \(M\) sont au milieu du segment.
Le point \(M\) est le milieu de \([AB]\).
\(MA = MB\)
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous bien la définition et les propriétés de la médiatrice d'un segment?
La médiatrice d’un segment est la droite qui le coupe perpendiculairement en son milieu.
Question 7
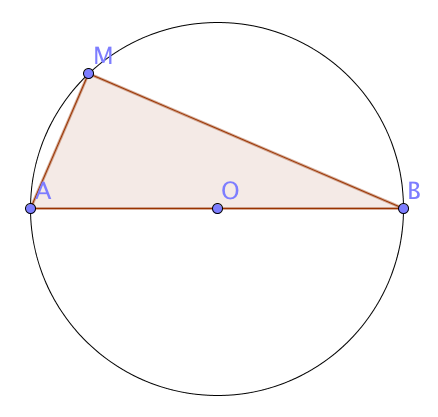
Dans la figure ci- dessus, cochez la MAUVAISE réponse :
\(AMB\) est rectangle en \(M\)
\(MA^2+BM^2=AB^2\)
\( OA = OB = OM\)
Une des trois réponses précédentes est fausse.
Attention, il faut cocher la réponse fausse.
Vous allez devoir faire preuve d’une logique implacable.
Question 8
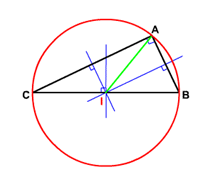
On a tracé les trois médiatrices du triangle \(ABC\) inscrit dans le cercle de diamètre \([BC]\). Cochez la MAUVAISE réponse.
\(I\) est le milieu de \([CB]\).
\(I\) est le centre du cercle circonscrit au triangle \(ABC\).
\(IA^2+BI^2=AB^2\)
Certaines des trois réponses précédentes sont exactes.
Tout ce qui n’est pas faux est vrai.
Question 9
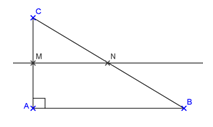
Dans le triangle ci dessus, \(M\) et \(N\) sont les milieux respectifs des segments \([CA]\) et \([CB]\).
Cochez la bonne réponse :
\(\dfrac{CM}{MA}=\dfrac{CN}{NB}=\dfrac{MN}{AB}\)
\(MN = AC\)
\(AB = 2MN\)
Aucune des trois réponses précédentes n’est exacte.
Vous souvenez-vous de la propriété de la droite des milieux ?
Regardez la vidéo de rappel. Vous pouvez aussi utiliser Thalès pour conclure.
Question 10
Dans ce triangle, on a :
\(sin (Â) = \dfrac{o}{h}\)
\(sin (Â) = \dfrac{AB}{AC}\)
\(sin (Â) = \dfrac{CA}{CB}\)
Aucune des trois réponses précédentes n’est exacte.
Il y a des formules à savoir par cœur. Celle-ci en est une.
Voulez-vous revoir cette vidéo sur le sinus d’un angle dans le triangle rectangle. Regardez la vidéos de rappel.