Démontrer, pour chacune des trois figures ci-dessous, que le triangle $ABC$ est un triangle rectangle en utilisant les infirmations fournies.
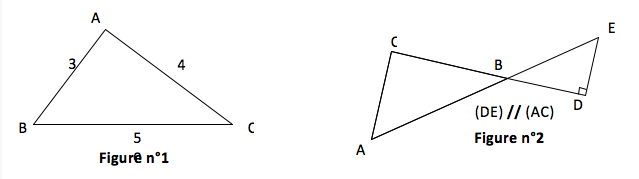
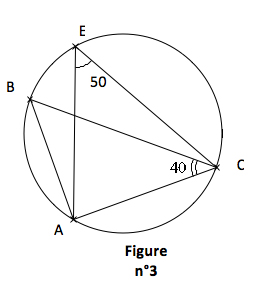
Figure 1
D'une part la somme des carrés des deux plus petits côtés est :
$AB^2 + AC^2 = 30^2 + 40^2 = 900 + 1600 = 2500$
D'autre part le carré du plus grand côté est :
$BC^2 = 50^2 = 2500$
Puisque $AB^2 + AC^2 = BC^2$, alors d'après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $A$.
Figure 2
Si deux droites sont parallèles, alors toute perpendiculaire à l'une est perpendiculaire à l'autre.
Ici $(DE) \ // \ (AC)$ et $(CD) \perp (DE)$ donc $(CD) \perp (AC)$.
Puisque $(CD) \perp (AC)$, alors $\widehat{ACB} = 90°$ et le triangle $ABC$ est rectangle en $C$.
Figure 3
Puisque les deux angles $\widehat{ABC}$ et $\widehat{AEC}$ sont inscrits dans le même cercle et interceptent le même arc $\overset{\frown}{AC}$, alors ils ont la même mesure : $\widehat{ABC} = \widehat{AEC} = 50°$
Dans le triangle $ABC$, les angles $\widehat{ABC}$ et $\widehat{ACB}$ sont complémentaires $(\widehat{ABC} + \widehat{ACB} = 50° + 40° = 90°)$.
Donc $\widehat{BAC} = 90°$ et le triangle $ABC$ est rectangle en $A$.
