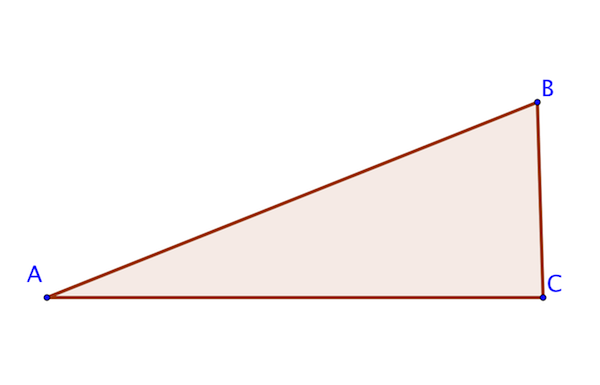
L'énoncé
Tu as obtenu le score de
Question 1
On veut savoir si le triangle est rectangle. Quelle doit-être la première étape de notre recherche ?
On trace en vraie grandeur et on vérifie avec une équerre.
On compare \(AB\) et \(AC + BC\)
On compare \(AB^2\) et \(AC^2 + BC^2\)
On compare \(AB\) et \((AC + BC)^2\)
Oubliez l’équerre ! Vous n’êtes plus en 6e ! Il s’agit ici de trouver une preuve scientifique. Quelque chose d’irréfutable !
Ce sont les carrés de chaque longueur qui sont importants !
Question 2
On va donc calculer \(AB^2\) et \(AC^2 + BC^2\)
Quels sont les bons résultats ?
\(AB^2 = 32\ \) et \(\ AC^2 + BC^2 = 44\)
\(AB^2 = 256\ \) et \(\ AC^2 + BC^2 = 256\)
\(AB^2 = 250\ \) et \(\ AC^2 + BC^2 = 260\)
\(AB^2 = 256\ \) et \(\ AC^2 + BC^2 = 260\)
\(16^2 = 16\times 16...\)
\(14^2 + 8^2 = 196 + 64 = …\)
Question 3
On a donc : \(AB^2 = 256\ \) et \(\ AC^2 + BC^2 = 260\)
On se demande toujours si le triangle est rectangle ou non.
Voilà le cas inhabituel, celui que vous rencontrez rarement, néanmoins ça arrive ! Il va falloir sen sortir et conclure
Quel théorème va nous permettre de conclure ?
Le théorème de Thalès
Le théorème de Pythagore
La réciproque du théorème de Thalès
La réciproque du théorème de Pythagore
Thalès ? Bien sûr que non…
Attention piège ! La réciproque du théorème de Pythagore nous dit ce qu’il se passe lorsque \(AB^2 = AC^2 + BC^2\),
Mais elle ne dit rien dans le cas contraire !
Question 4
Le mathématicien Héron dAlexandrie (Ier siècle), a trouvé une formule permettant de calculer l'aire dun triangle. En notant a, b et c les longueurs des trois côtés et p son périmètre, l'aire du triangle est donnée par la formule : \(Aire_{Triangle}=\sqrt{\dfrac{p}{2}\left(\dfrac{p}{2}-a\right)\left(\dfrac{p}{2}-b\right)\left(\dfrac{p}{2}-c\right)}\)
Mais commençons en douceur : puisque nous allons en avoir besoin, calculons le périmètre du triangle ABC.
À combien est égal le périmètre \(p\) du triangle ABC ?
\(p = AB \times AC \times BC = 16 \times 14 \times 8 = 1792\)
\(p=AB + AC + BC = 16 + 14 + 8 = 38\)
\(p=2 \times(AC + BC) = 2 \times (14 + 8) = 2 \times 22 = 44\)
J’ai besoin de la formule du périmètre du triangle.
Pour le triangle, pas de formule ! Il suffit d’ajouter les longueurs des 3 côtés.
C’est-à-dire : \(AB + AC + BC\)
Question 5
Maintenant que l'on sait que $p = 38$, que devient la formule de Héron lorsque l'on remplace par les valeurs numériques ?
$Aire_{Triangle}=\sqrt{\dfrac{p}{2}\left(\dfrac{p}{2}-a\right)\left(\dfrac{p}{2}-b\right)\left(\dfrac{p}{2}-c\right)}$
\(Aire_{Triangle}=\sqrt{\dfrac{38}{2}\left(\dfrac{38}{2}-a\right)\left(\dfrac{38}{2}-b\right)\left(\dfrac{38}{2}-c\right)}\)
\(Aire_{Triangle}=\sqrt{38(38-16)(38-14)(38-8)}\)
\(Aire_{Triangle}=\sqrt{\dfrac{38}{2}\left(\dfrac{38}{2}-16\right)\left(\dfrac{38}{2}-14\right)\left(\dfrac{38}{2}-8\right)}\)
\(Aire_{Triangle}=\sqrt{\dfrac{p}{2}\left(\dfrac{p}{2}-16\right)\left(\dfrac{p}{2}-14\right)\left(\dfrac{p}{2}-8\right)}\)
p = 38, AB = 16, AC = 14 et BC = 8.
Dans la formule, il y a les longueurs a, b et c… Ce sont les longueurs des trois côtés du triangle, c’est-à-dire ici AB, AC et BC.
Question 6
On a donc :
\(Aire_{Triangle}=\)
\(\sqrt{\dfrac{38}{2}\left(\dfrac{38}{2}-16\right)\left(\dfrac{38}{2}-14\right)\left(\dfrac{38}{2}-8\right)}\)
Quelle est l'étape suivante du calcul ? Pensez à simplifier votre résultat.
\(Aire_{Triangle}=\sqrt{19(19-16)(19-14)(19-8)}\)
\(Aire_{Triangle}=\sqrt{\dfrac{38(38-16)(38-14)(38-8)}{2}}\)
\(Aire_{Triangle}=\sqrt{\dfrac{38}{2}\left(\dfrac{38}{2}-\dfrac{32}{2}\right)\left(\dfrac{38}{2}-\frac{28}{2}\right)\left(\dfrac{38}{2}-\dfrac{16}{2}\right)}\)
\(Aire_{Triangle} = \sqrt{\dfrac{38}{2}\times \dfrac{38}{2}-16\times \dfrac{38}{2}-14\times \dfrac{38}{2}-8}\)
\(\dfrac{38}{2}=19 \)… Ça va grandement simplifier les écritures.
Et la division est prioritaire.
Question 7
On a donc :
\(Aire_{Triangle}=\sqrt{19(19-16)(19-14)(19-8)}\)
Quelle est l'étape suivante du calcul ?
\(Aire_{Triangle}=\sqrt{19(19-16-14-8)}\)
\(Aire_{Triangle}=\sqrt{(19^2-19\times 16)(19-14)(19-8)}\)
\(Aire_{Triangle}=\sqrt{19\times 19-16\times 19-14\times 19-8}\)
\(Aire_{Triangle}=\sqrt{19\times 3\times5\times11}\)
Dans un calcul numérique, on commence toujours par les parenthèses.
(19 – 16) … (19 – 14) … Ça va c’est pas trop corsé, non ?
Question 8
On a donc : \(Aire_{Triangle}=\sqrt{19\times 3\times5\times11}\). Quelle est l'étape suivante du calcul ?
\(Aire_{Triangle}=\sqrt{38}\)
\(Aire_{Triangle}=\sqrt{3135}\)
\(Aire_{Triangle}= 3135\)
\(Aire_{Triangle}= \sqrt{19} \times \sqrt{3} \times \sqrt{5} \times \sqrt{11} \)
Priorité ? Le produit !
Il faut vous tenir la calculatrice ou vous y arrivez tout seul ? ;-)
Question 9
On a donc : \(Aire_{Triangle}=\sqrt{3135}\). Quelle est l'aire du triangle ?
(On donnera une valeur approchée à l'unité.)
\(Aire_{Triangle} \approx 55 \ cm^2\)
\(Aire_{Triangle} \approx 56 \ cm^2\)
\(Aire_{Triangle} \approx 55,9 \ cm^2\)
\(Aire_{Triangle} \approx 55,99 \ cm^2\)
À l’unité, c’est-à-dire au chiffre des unités !
Attention, le chiffre des dixièmes est 9.