L'énoncé
Dans le cadre d’un projet pédagogique, des professeurs préparent une sortie au Mont Saint-Michel avec les $48$ élèves de Troisième.
Deux activités sont au programme :
- La visite du Mont Saint-Michel et de son abbaye ;
- La traversée à pied de la baie du Mont Saint-Michel.
Le coût total de cette sortie (bus, hébergement et nourriture, activités, …) s’élève à $120\ €$ par élève.
Question 1
Alexandre souhaite savoir à quelle distance il se trouve du Mont à l’aide d’un théodolite (appareil servant à mesurer des angles). Il sait que le sommet du Mont est à $170\ m$ d’altitude. Son œil ($O$ sur le dessin) étant situé à $1,60\ m$ du sol, il obtient la mesure suivante :
$SOH= 25°$ (Le dessin n’est pas réalisé à l’échelle).
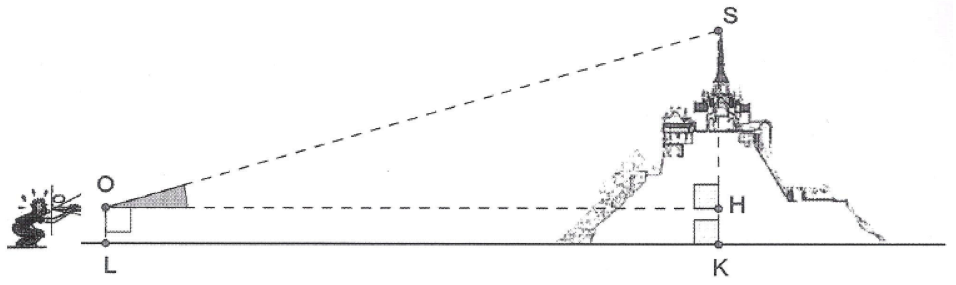
À quelle distance $LK$ du mont se trouve-t-il ? (Donner une valeur approchée au mètre).
$OHKL$ étant un rectangle, il suffira de trouver $OH$ (car $OH = LK$) et d'enlever $1,6 \ m$ à $SK$ pour obtenir $SH$.
Donc dans le triangle, rectangle en $H$, $OSH$, on peut utiliser la tangente de l'angle $SOH$ :
$\tan SOH = \dfrac{SH}{OH} = \dfrac{170 - 1,6}{OH}$
Donc $\tan 25° = \dfrac{168,4}{0H}$ et $OH = \dfrac{168,4}{\tan 25°}$
Soit environ $361 \ m$ à $1 \ m$ près.
Question 2
En utilisant le plan ci-après on peut dire que la superficie de la partie émergée du mont se situe :
Entre $10 000 \ m^2$ et $40 000 \ m^2$ ;
Entre $40 000 \ m^2$ et $80 000 \ m^2$ ;
Entre $80 000 \ m^2$ et $150 000 \ m^2$ ;
Entre $150 000 \ m^2$ et $200 000 \ m^2$.
Quelle est la bonne réponse ? Justifier.

En utilisant le plan on peut dire que la superficie de la partie émergée du Mont se situe entre $40000 \ m^2$ et $80000\ m^2$.
On peut faire tenir le plan de la ville dans un rectangle de :
$17 \ \text{carreaux de large} \times 20 \ \text{carreaux de haut}$
Cela correspond à une aire de $A = 15^2 \times 17 \times 20 = 76500 \ m^2$
L'aire est aussi supérieure à une somme de $200$ petits carreaux soit $45000 \ m^2$
