Prendre une feuille et un crayon et répondre aux questions suivantes.
Un fabricant d'enseignes lumineuses doit réaliser la lettre Z (en tubes de verre soudés) pour la fixer sur le haut d'une vitrine. Voici le schéma donnant la forme et certaines dimensions de l'enseigne :
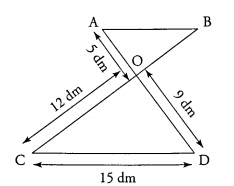
Les droites $(AD)$ et $(BC)$ se coupent en $O$.
1) Sachant que les droites $(AB)$ et $(CD)$ sont parallèles, calculer la longueur $OB$.
2) Démontrer que le tube $[BC]$ est perpendiculaire à la droite $(AD)$.
3) Calculer la mesure de l’angle $\widehat{OCD}$ (donner une valeur arrondie au degré près).
1) On considère les triangles $AOB$ et $OCD$, on a :
$A \in (OD) ; \ B \in (OC)$ et $(AB)\ // \ (CD)$ ; donc d’après le théorème de Thalès :
$\dfrac{AO}{OD}=\dfrac{OB}{OC}=\dfrac{AB}{CD}$ soit
$\dfrac{5}{9}=\dfrac{OB}{12}$
Donc : $OB = \dfrac{5\times 12}{9}$
Finalement : $OB =\dfrac{20}{3}$ dm.
2) On considère le triangle $OCD , \ [CD]$ est le plus grand côté :
$OC^2+OD^2=12^2+9^2=144+81=225$
Donc $CD^2= OC^2+OD^2$
Ainsi, d’après la réciproque du théorème de Pythagore le triangle $OCD$ est rectangle en $O$.
On en déduit que $(OC)$ est perpendiculaire à $(OD)$.
Or $A,O,D$ sont alignés ainsi que $B, O, C$ donc le tube $[BC]$ est perpendiculaire à la droite $(AD)$.
3) Dans le triangle $OCD$ rectangle en $O$, on peut écrire :
$cos(\widehat{OCD})=\dfrac{OC}{CD}$
Soit : $cos(\widehat{OCD}) =\dfrac{12}{15}$
Donc : $\widehat{OCD}\approx 37°$ (arrondi au degré près).
