On considère un triangle $ABC$ tel que : $AB = 17,5$ cm ; $BC = 14$ cm ; $AC = 10,5$ cm.
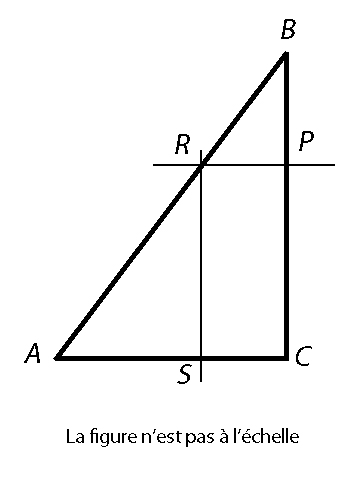
Partie 1
1) Démontrer que le triangle $ABC$ est rectangle en $C$.
2) Soit $P$ un point du segment $[BC]$.
La parallèle à la droite $(AC)$ passant par $P$ coupe le segment $[AB]$ en $R$.
La parallèle à la droite $(BC)$ passant par $R$ coupe le segment $[AC]$ en $S$.
Montrer que le quadrilatère $PRSC$ est un rectangle.
3) Dans cette question, on suppose que le point $P$ est situé à $5$ cm du point $B$.
A) Montrer que la longueur $PR$ est égale à $3,75$ cm.
B) Quelle est la longueur de $PC$ ?
C) Calculer l’aire du rectangle $PRSC$.
Partie 2
On déplace le point $P$ sur le segment $[BC]$ et on souhaite savoir quelle est la position du point $P$ pour laquelle l’aire du rectangle $PRSC$ est maximale.
1) L’utilisation d’un tableur a conduit au tableau de valeurs suivant :
|
Longueur $BP$ en cm |
$0$ |
$1$ |
$3$ |
$5$ |
$8$ |
$10$ |
$12$ |
$14$ |
|
Aire de $PRSC$ en cm$^2$ |
$0$ |
$9,75$ |
$24,75$ |
$…$ |
$36$ |
$…$ |
$18$ |
$0$ |
A) Indiquer sur la copie les deux valeurs manquantes du tableau.
B) Justifier par un calcul la valeur trouvée pour BP = 10 cm.
2) Un logiciel a permis d’obtenir la représentation graphique suivante :
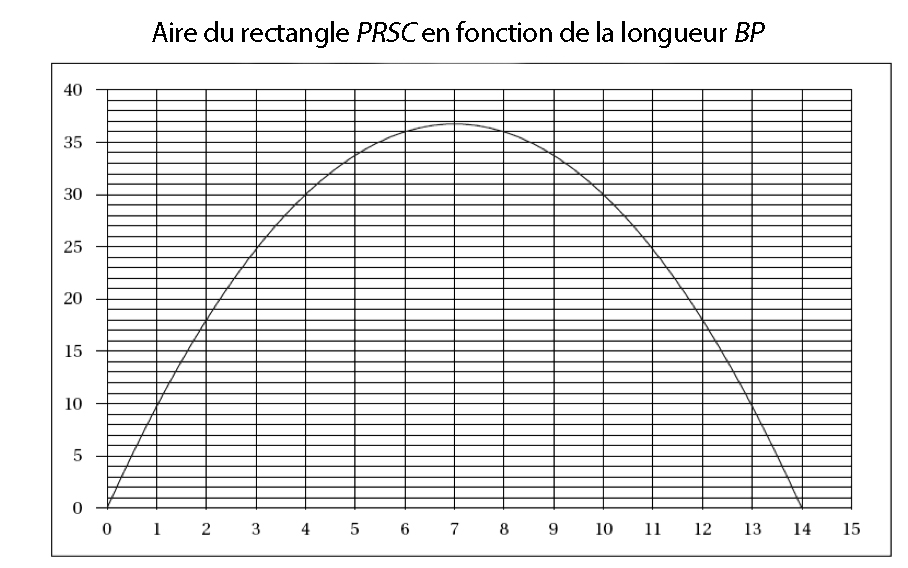
À l’aide d’une lecture graphique, répondre aux questions en faisant apparaître sur le graphique de la feuille ci-dessus les tracés nécessaires.
A) Les valeurs de $BP$ pour lesquelles le rectangle $PRSC$ a une aire de $18$ cm$^2$.
B) La valeur de $BP$ pour laquelle l’aire du rectangle semble maximale.
C) Un encadrement à $1$ cm$^2$ près de l’aire maximale du rectangle $PRSC$.
Partie 3
1) Exprimer $PC$ en fonction de $BP$.
2) Démontrer que $PR$ est égale à $0,75 \times BP$.
3) Pour quelle valeur de $BP$ le rectangle $PRSC$ est-il un carré ?
Partie 1
1) Dans le triangle $ABC$,
$\left. \begin{array}{ll}{ AB^2 = 17,5^2 = 306,25 \\ AC^2 + BC^2 = 10,5^2 + 14^2 = 306,25} \end{array} \right\} AB^2 = AC^2 + BC^2$
D'après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $C$.
2) On sait que $(RP) \ // \ (SC)$ et $(RS) \ // \ (CP) $
Un quadrilatère dont les côtés opposés sont parallèles est un parallélogramme.
Donc $PRSC$ est un parallélogramme.
On sait que $\widehat{BCA} = 90°$ donc par construction, $\widehat{PCS} = 90°$
Or un parallélogramme qui possède un angle droit est un rectangle.
Donc $PRSC$ est un rectangle.
3) A) $R \in (BA), P \in (BC)$ et $(RP) \ // \ (AC)$
D'après le théorème de Thalès, on obtient : $\dfrac{BP}{BC} = \dfrac{RP}{AC}$ soit $\dfrac{5}{14} = \dfrac{RP}{10,5}$
Donc $ RP = \dfrac {5\times 10,5}{14}$ soit $ RP = 3,75$ cm.
B) L'aire du rectangle $PRSC$ est égale à $RP \times PC$
$P$ appartient à $[BC]$ donc $BC = BP + PC$
et donc $PC = BC - BP = 14 -5 = 9$. $PC = 9$ cm.
Donc $A \ (PRSC) = 3,75 \times 9 = 33, 75$ cm$^2$
Partie 2
1) D'après la partie 1 du problème, si $BP = 5$ alors $A \ (PRSC) = 33,75$ cm$^2$
Si $BP = 10$ :
$RP = \dfrac{BP \times AC}{BC} = \dfrac{10 \times 10,5}{14} = 7,5$ cm
$PC = BC-BP = 14-10 = 4$ cm
Donc $A \ (PRSC) = 7,5 \times 4 = 30$ cm$^2$
2) A) L'aire du rectangle est égale à $18$ cm$^2$ pour une valeur de $BP$ égale à $2$ cm ou $12$ cm.
B) La valeur de l'aire du rectangle semble maximale pour $BP = 7$ cm.
C) $36$ cm$^2 < $ aire maximale $ < 37$ cm$^2$
Partie 3
1) $PC = BC - BP = 14 - BP$
2) D'après le théorème de Thalès (partie 1) :
$\dfrac{PR}{AC} = \dfrac{BP}{BC}$
Donc $PR = \dfrac{BP \times AC}{BC} = \dfrac{10,5}{14}$ soit $BP = 0,75$
3) $PRSC$ est un caré lorsque $PR = PC$. C'est-à-dire lorsque $0,75 BP = 14 - BP$
$PB = \dfrac{14}{1,75} = 8$
$PRSC$ est donc un carré lorsque $PB = 8$ cm.
