L'énoncé
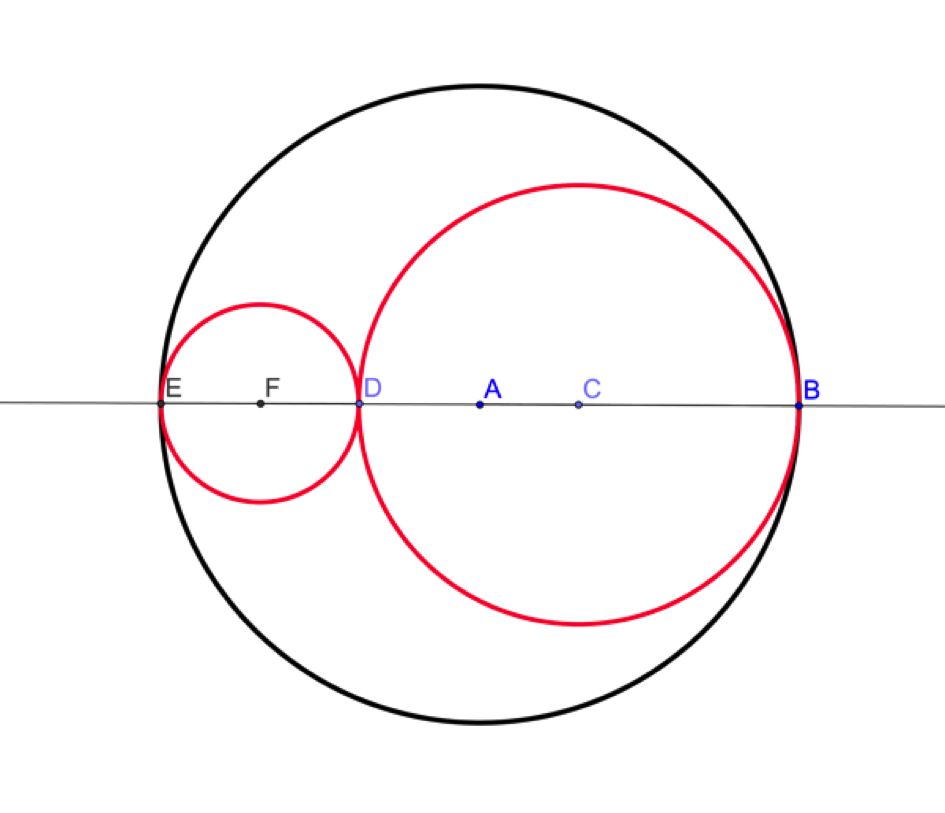
Pour équiper un nouveau quartier d’une ville, on enterre un tuyau cylindrique représenté en coupe ci-dessous par le disque \(D_1\) de diamètre \([BE]\) et de centre \(A.\) On souhaite y installer une canalisation d’eau (représentée en coupe par le disque \(D_2\) de diamètre \([BD]\) et de centre \(C\)) et un câble électrique (représenté en coupe par le disque \(D_3\) de diamètre \([DE]\) de centre \(F\)).
On donne \(BE = 70 \ cm\) et \(BC = x.\)
On cherche la valeur de \(x\) pour laquelle l’aire occupée par la section des deux petits cylindres représente 50% de l’aire de la section du tuyau.
Question 1
Quelles sont les valeurs possibles du nombre \(x\) ?
\(x\) est une longueur donc positif.
De plus, le disque de diamètre \([BD]\) sera confondu avec le disque de diamètre \([BE]\) lorsque son diamètre vaut 70 cm, c'est à dire lorsque \(2x = 70\).
Ainsi \(x =35\) est la valeur maximale de cette longueur.
Conclusion : \(x\) appartient à l'intervalle \([0 ; 35]\).
Attention \(x\) est une longueur.
Cherchez les dimensions limites du disque de diamètre \([BD].\)
Question 2
Calculez la valeur exacte de l'aire \(A_{D_1}\) du disque de diamètre \([BE]\).
\(A_{D_1} = \pi \times AB^2\)
\(A_{D_1} = 35^2 \times \pi\)
\(A_{D_1} = 1225 \pi \text{ cm}^3\)
Il faut connaître l’aire d’un disque de rayon \(R.\) Un oubli ? Il y a le nombre \(\pi\) dans la formule.
\(A = \pi R^2\)
Question 3
Exprimez \(FD\) le rayon du disque \(D_3\) en fonction de \(x\).
On a :
\(DE = BE-BD\)
\( DE= 70 2x\)
Ainsi :
\(FD = \dfrac{(70-2x)}{2}\)
\(FD = 35-x\)
\(FD = \dfrac{DE}{2}\)
\(DE = BE-BD\)
Question 4
Exprimez en fonction de \(x\) la somme des aires des disques \(D_2\) et \(D_3.\) On notera \(S(x)\) cette expression.
\(S(x) = \pi \times x^2 + \pi(35-x)^2\)
\(S(x) = \pi(x^2 +35^2-2 \times 35x+x^2)\)
\(S(x) = \pi(2x^2-70x+1225)\)
Calculez l’aire de chaque disque en fonction de \(x\). Cela veut dire que vous aurez le nombre \(x\) (la variable) dans le résultat.
Additionnez ensuite ces deux aires.
Question 5
Cherchons la valeur de \(x\) pour laquelle l'aire occupée par la section des deux petits cylindres représente 50% de l'aire de la section du tuyau.
Écrivez l'équation traduisant ce problème et vérifiez qu'elle s'écrit aussi sous la forme : \(2(x-17,5)^2 = 0\).
On souhaite que \(s(x) = \dfrac{50}{100} \times A_{D_1}\)
Ainsi : \(\pi(2x^2-70x+1225)= 0,5 \times 1225\pi\)
En simplifiant par \(\pi\) , il vient :
\(2x^2-70x+1225 = 612,5\)
\(2x^2-70x+1225-612,5 = 0\)
\(2x^2-70x +612,5 = 0\)
Or en développant l'égalité remarquable \(2(x-17,5)^2\)
On trouve l'expression \(2x^2-70x +612,5\).
Ainsi l'équation équivaut à :
\(2(x-17,5)^2 = 0\)
Ou encore en simplifiant par deux :
\((x-17,5)^2 = 0\)
Traduisez cette phrase avec les données du problème.
Pour calculer 50% d’un nombre, vous multipliez ce nombre par 0,5.
Question 6
Résolvez à présent : \((x-17,5)^2 = 0\).
\((x-17,5)^2 = 0\) équivaut à \((x-17,5) = 0\)
Finalement, on a :
\(x = 17,5\)
Conclusion: lorsque \(x\) vaut 17,5 cm, l'aire occupée par la section des deux petits cylindres représente 50% de l'aire de la section du tuyau.
À quelle condition le carré d’un nombre est-il nul ?
Si le nombre est nul bien sûr.
