1
Video
Fonctions linéaires et affines
2
Exercice
Devoir sur feuille
3
Video
Fonction carré
4
Exercice
QCM - La fonction carré
5
Video
Fonction racine carrée
6
Video
Fonction inverse
7
Exercice
Devoir sur feuille
8
Video
Fonction du second degré - Le rappel de cours
9
Exercice
QCM - Second degré
10
Exercice
Exercice - Second degré et aires de disques
11
Video
Fonctions homographiques - Le rappel de cours
12
Exercice
QCM - Fonctions homographiques
Accède gratuitement à cette vidéo pendant 7 jours
Profite de ce cours et de tout le programme de ta classe avec l'essai gratuit de 7 jours !
Fiche de cours
Fonction inverse
Définition
Pour tout $x \in \mathbb{R}^*$, la fonction inverse est la fonction définie par $f(x) = \dfrac{1}{x}$.
On remarquera que l'ensemble de définition de la fonction inverse est $\mathbb{R}^*$ ou encore $\left]-\infty;0\right [\cup \left]0;+\infty\right[$ car on ne peut pas diviser par 0.
La représentation graphique de la fonction inverse est une hyperbole.
Chaque point de la courbe est le symétrique d'un autre par la symétrie centrale de centre $O(0;0)$ : la fonction inverse est une fonction impaire.
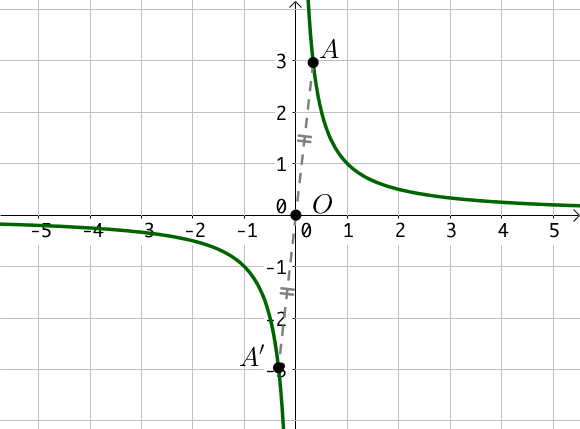
Variations
La fonction inverse est décroissante pour $x$ strictement négatif et décroissante pour $x$ strictement positif.
Son tableau de variation est le suivant :
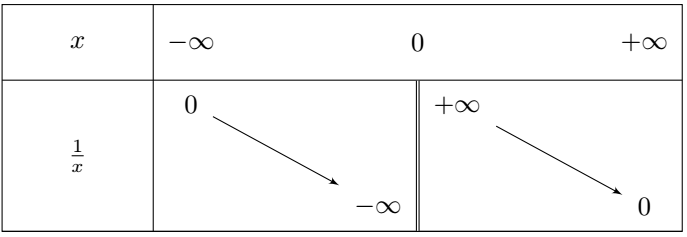
La double barre utilisée signifie que $0$ est une valeur in
Il reste 70% de cette fiche de cours à lire
Cette fiche de cours est réservée uniquement à nos abonnés. N'attends pas pour en profiter, abonne-toi sur
lesbonsprofs.com. Tu pourras en plus accéder à l'intégralité des rappels de cours en vidéo ainsi qu'à des QCM et des exercices d'entraînement avec corrigé en texte et en vidéo.
