L'énoncé
Cet exercice est un QCM. Une seule réponse est exacte. Nous allons aborder plusieurs fonctions dans des repères orthonormés. Chaque fonction devra être écrite sous la forme \(f(x) = a(x-\alpha)^2 + \beta\) pour appliquer le cours.
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
On considère la fonction
\(f(x) = x^2 - 2x +5\), définie sur $\mathbb{R}$.
La forme canonique de \(f\) est :
\( f(x) = (x-1)^2 +5\)
\(f(x) = (x+1)^2 +5\)
\(f(x) = (x-1)^2 +4\)
\(f(x) = (x+1)^2 +4\)
\(x^2 – 2x\) est le début d’un égalité remarquable. Laquelle ?
Il s’agit d’une expression de la forme \((a-b)^2\).
Remarquez alors que \(5 = 4+1\) pour conclure.
Question 2
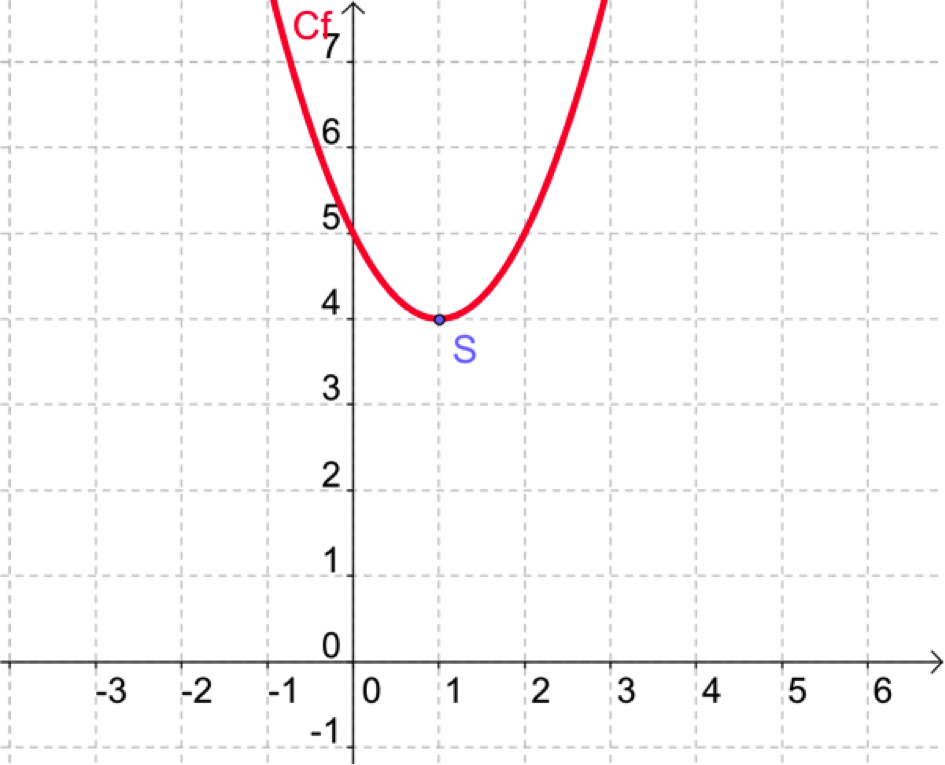
\(f(x) = (x-1)^2 +4\)
Quelle est la représentation graphique de cette fonction ?
Une parabole, branches dirigées vers le bas.
Une hyperbole, branches dirigées vers le haut.
Une hyperbole, branches dirigées vers le bas.
Une parabole, branches dirigées vers le haut.
C’est du cours. Le connaissez-vous parfaitement ? Vous pouvez revoir la vidéo sur le second degré dans les prérequis.
Ne confondez par les paraboles (fonction carré) et hyperboles (fonction inverse) que vous avez vues en classe.
La réponse dépend du signe du terme précédent la parenthèse.
Ici : c’est le nombre 1 car \(f(x) = 1 \times (x-1)^2 +4\). Quel est son signe ?
Question 3
\(f(x) = (x-1)^2 +4\)
Quelles sont les coordonnées du sommet $S$ de la parabole ?
\(S(1 ;4)\)
\(S(-1 ;4)\)
\(S(1 ;-4)\)
\(S(-1 ;-4)\)
C’est encore du cours. Revoyez le avant de répondre.
Si \(f(x) = a(x-\alpha)^2+\beta\) alors le sommet de la parabole est \(S(\alpha;\beta)\).
Quelles sont ici les valeurs de \(\alpha\) et \(\beta\) ? Attention aux signes !
Question 4
\(f(x) = (x-1)^2 +4\). Le sommet de la parabole est \(S(1 ;4)\).
Cochez la bonne réponse :
La fonction \(f\) est croissante sur \([4, +\infty[\).
La fonction \(f\) est décroissante sur \([1, +\infty[\).
La fonction \(f\) est croissante sur \([1, +\infty[\).
La fonction \(f\) est décroissante sur \([4, +\infty[\).
Tracez la courbe dans un repère, cela vous aidera.
N’oubliez pas, les branches de la parabole sont dirigées vers le haut.
Si vous avez oublié ce qu’est une fonction croissante, regardez la vidéo dans le chapitre : « Généralités sur les fonctions ».
Question 5
\(f(x) = (x-1)^2 +4\). Le sommet de la parabole est \(S(1 ;4)\).
Cochez la bonne réponse :
Le minimum de \(f\) est 1.
Le maximum de \(f\) est 4.
\(f\) n’a pas de minimum.
Le minimum de \(f\) est 4.
Savez-vous ce qu’est le minimum d’une fonction ? Revoyez bien la vidéo du cours dans le chapitre "Généralités d'une fonction".
Imaginez que ce soit une courbe de température. Que répondriez-vous ?
Voici la représentation graphique de \(f\) :
Question 6
On considère la fonction :
\(g(x) = -4x^2-16x-13\), définie sur \(\mathbb{R}\).
La forme canonique de \(g\) est :
\(g(x) = -4(x-2)^2 +3\)
\(g(x) = (4x+2)^2 +3\)
\( g(x) = -4(x-2)^2 -3\)
\( g(x) = -4(x+2)^2 +3\)
Factorisez les deux premiers termes par -4.
\(x^2 +4x\) est le début d’un égalité remarquable. Laquelle ?
Il s’agit d’une expression de la forme \((a+b)^2\).
Équilibrez votre expression pour retrouver celle de \(g\).
Question 7
On sait que \(g(x) = -4(x+2)^2 +3\).
Quelle est la représentation graphique de cette fonction ?
Une parabole, branches dirigées vers le bas.
Une hyperbole, branches dirigées vers le haut.
Une hyperbole, branches dirigées vers le bas.
Une parabole, branches dirigées vers le haut
C’est du cours. Le connaissez-vous parfaitement ? Vous pouvez revoir la vidéo dans les prérequis.
La réponse dépend du signe du terme précédent la parenthèse.
Ici : c’est le nombre -4 car \(f(x) = -4(x+2)^2 +3\). Quel est son signe ?
Question 8
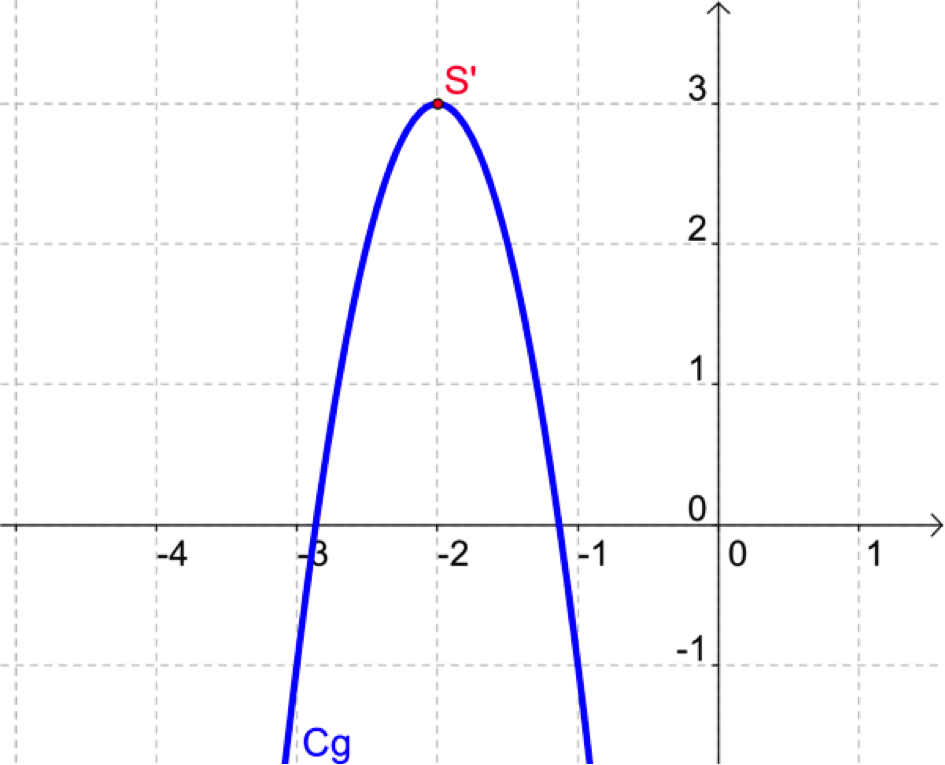
\(g(x) = -4(x+2)^2 +3\)
Quelles sont les coordonnées du sommet \(S'\) de la parabole ?
\(S’(2 ;-3)\)
\(S’(-2 ;-3)\)
\(S’(-2 ;3)\)
\(S’(2 ;3)\)
C’est encore du cours. Revoyez-le avant de répondre.
Si \(g(x) = a(x-\alpha)^2+\beta\) alors le sommet de la parabole est \(S'(\alpha;\beta)\).
Quelles sont ici les valeurs de \(\alpha\) et \(\beta\) ? Attention aux signes !
Question 9
\(g(x) = -4(x+2)^2 +3 \). Le sommet de la parabole est \(S(-2 ;3)\).
Cochez la bonne réponse :
La fonction \(g\) est croissante sur \([-2, +\infty[\).
La fonction \(g\) est décroissante sur \([-3, +\infty[\).
La fonction \(g\) est croissante sur \([3, +\infty[\).
La fonction \(g\) est décroissante sur \([-2, +\infty[\).
Tracez la courbe dans un repère, cela vous aidera.
N’oubliez pas, les branches de la parabole sont dirigées vers le haut.
Si vous avez oublié ce qu’est une fonction croissante, regardez la vidéo dans le chapitre : « Généralités sur les fonctions ».
Question 10
\(g(x) = -4(x+2)^2 +3 \). Le sommet de la parabole est \(S(-2 ;3)\).
Cochez la bonne réponse :
Le maximum de \(g\) est -2.
Le maximum de \(g\) est 3.
\(g\) n’a pas de maximum.
Le minimum de \(g\) est -2.
Savez-vous ce qu’est le maximum d’une fonction ? Revoyez la vidéo du cours.
Imaginez encore que ce soit une courbe de température. Que répondriez vous ?
Voici une représentation graphique de la fonction \(g\) :