L'énoncé
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x) = |x - 1| - | - 2x + 4|\).
Question 1
Donner l'expression de \(f(x)\) sans valeur absolue.
Pour \(x \leq 1, f(x) = x -3\)
Pour \(x \in [1 ; 2], f(x) = 3x -5\)
Pour \(x \geq 2, f(x) = - x + 3\)
Écris d'abord \(|x – 1|\). Ensuite écris \(| - 2x + 4|\) puis \(- | - 2x + 4|\).
Réunis ces résultats dans un tableau.
Question 2
Calculer l'image de \(-2\) par \(f\).
\(f(-2) = |-2 -1| - | - 2\times(-2) + 4|\)
\(f(-2)= |-3|-| 8 | \)
\(f(-2)= 3 - 8 \)
\(f(-2)= - 5 \)
L'image de \(-2 \) par \(f \) est \( 5 \).
L'image de \(-2\) est \(f(-2)\).
Attention aux signes !
Question 3
Dresser le tableau des variations de \(f\) sur \(\mathbb{R}\) :
\(f(1) = - 2\) et \(f(2) = 1\)
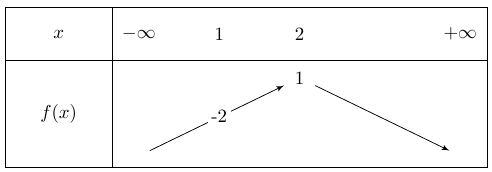
On a l'expression de \(f\) sur 3 intervalles différents.
Sur chaque intervalle \(f\) est une fonction affine, donc on connait ses variations.
Question 4
Tracer la représentation graphique de \(f\) dans un repère du plan.
Tracer la représentation de chacune des trois fonctions affines sur son ensemble de définition.
Question 5
Résoudre sur \(\mathbb{R}\) l'équation \(f(x) = - 3\).
Pour \(x \leq 1, f(x) = x -3\) donc
\(f(x) = - 3 \Leftrightarrow x -3 = - 3\)
\( \Leftrightarrow x = 0\)
\(0 \leq 1\) donc \( S_1 = \{ 0 \}\)
Pour \( x \in [1 ; 2], f(x) = 3x -5 \) donc
\(f(x) = - 3 \Leftrightarrow 3x-5 = - 3\)
\( \Leftrightarrow x = \dfrac{2}{3}\)
or, \(\dfrac{2}{3} \notin [1 ; 2]\) donc pas de solution sur cet intervalle.
Pour \(x \geq 2, f(x) = - x + 3\) donc
\(f(x) = - 3 \Leftrightarrow -x + 3 = - 3 \)
\( \Leftrightarrow x = 6\)
\(6 \geq2 \) donc \(S_2 = \{ 6 \}\)
Conclusion : l'ensemble des solutions sur \(\mathbb{R}\) de \(f(x) = -3 \) est \(S = \{ 0 ; 6\}\).
Résous alors les équations sur chacun des 3 intervalles. Attention de bien vérifier que la valeur de \(x \)obtenue appartient bien à l'intervalle !
Encore une fois on connait l'expression de \(f(x)\) sur 3 intervalles distincts.
Question 6
Résoudre sur \(\mathbb{R}\) l'inéquation \(f(x) > - 3\).
Pour \(x \leq 1, f(x) > - 3 \Leftrightarrow x - 3 > - 3 \Leftrightarrow x > 0\) donc \( S_1 = ] 0 ; 1]\)
Pour \(x \in [1 ; 2], f(x) > - 3 \Leftrightarrow 3x 5 > - 3 \Leftrightarrow x > \dfrac{2}{3}\) donc \( S_1 = [1 ; 2]\)
Pour \(x \geq 2, f(x) > - 3 \Leftrightarrow -x + 3 > - 3 \Leftrightarrow x < 6\) donc \(S_2 = [2 ; 6[\)
Conclusion : l'ensemble des solutions sur \(\mathbb{R}\) de \(f(x) > - 3 \) est \(S = ] 0 ; 6[\)
Encore une fois on connait l'expression de \(f(x)\) sur 3 intervalles distincts.
Résoudre alors les inéquations sur chacun des 3 intervalles.
Attention de bien vérifier que les valeurs de \(x\) obtenues appartiennent bien à l'intervalle !