L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Des vidéos de rappel de cours sont aussi disponibles dans les prérequis.
Tu as obtenu le score de
Question 1
La représentation graphique de la fonction linéaire \(f\) telle que \(f(x) = 3x\) est
Une courbe.
Un point.
Une droite passant par le point \((0;3).\)
Une droite passant par l’origine du repère.
\(f(0) = 0\), par conséquent la représentation graphique de la fonction \(f\) passe par le point de coordonnées \((0;0)\).
Question 2
La droite passant par l'origine du repère et par le point de coordonnées \((1 ; 5)\) est la représentation graphique de la fonction \(f\) :
\(f(x) = 1x\)
\(f(x) = 1x + 5\)
\(f(x) = 5x\)
\(f(x) = x + 1\)
Si la représentation graphique de la fonction \(f\) est une droite passant par l’origine du repère, cela signifie que \(f\) est une fonction linéaire.
\(f\) est donc telle que \(f(x) = ax\) où \(a\) est un nombre à déterminer. Or la représentation graphique d’une fonction linéaire \(f\) passe par le point de coordonnée \((1;a)\).
Question 3
La droite passant par l'origine du repère et par le point de coordonnées \((2 ; 6)\) est la représentation graphique de la fonction \(f\) :
\(f(x) = 2x\)
\(f(x) = 3x\)
\(f(x) = 6x\)
\(f(x) = 2x + 6\)
Si la représentation graphique de la fonction \(f\) est une droite passant par l’origine du repère, cela signifie que \(f\) est une fonction linéaire.
\(f\) est donc telle que \(f(x) = ax\) où \(a\) est un nombre à déterminer. Or \(f(2) = 6\) ce qui signifie que \(a \times 2 = 6\).
Question 4
La représentation graphique de la fonction affine \(f\) telle que \(f(x) = 3x -1\) est :
Une droite passant par le point \((3;-1).\)
Une droite passant par le point \((0;3).\)
Une droite passant par le point \((0;-1).\)
Une droite passant par l’origine du repère.
La représentation graphique de la fonction affine \(f\) est une droite passant par le point d’abscisse 0 et d’ordonnée : « l’ordonnée à l’origine ».
Question 5
La droite ci-contre est la représentation graphique de la fonction \(f\) telle que :
\(f(x) = 2x\)
\(f(x) = 5x\)
\(f(x) = 10x\)
\(f(x) = x\)
Si la représentation graphique de la fonction \(f\) est une droite passant par l’origine du repère, cela signifie que \(f\) est une fonction linéaire.
\(f\) est donc telle que \(f(x) = ax\) , où \(a\) est un nombre à déterminer. Or la représentation graphique d’une fonction linéaire \(f\) passe par le point de coordonnée \((1;a)\).
Question 6
La droite ci-contre est la représentation graphique de la fonction \(f\) telle que :
\(f(x) = 2x\)
\(f(x) = -3x\)
\(f(x) = -x\)
\(f(x) = -2x\)
Si la représentation graphique de la fonction \(f\) est une droite passant par l’origine du repère, cela signifie que \(f\) est une fonction linéaire.
\(f\) est donc telle que \(f(x) = ax\) , où \(a\) est un nombre à déterminer. Or la représentation graphique d’une fonction linéaire \(f\) passe par le point de coordonnée \((1;a)\).
Question 7
La droite passant par le point de coordonnées \((0 ; 4)\) est la représentation graphique d'une fonction :
Linéaire
Affine
L’une ou l’autre, on ne peut pas savoir.
Ni linéaire, ni affine.
La représentation graphique d’une fonction linéaire \(f\) est une droite passant par l’origine du repère, or ici ce n’est pas le cas.
La représentation graphique de la fonction affine \(f\) est une droite passant par le point d’abscisse 0 et d’ordonnée : « l’ordonnée à l’origine ».
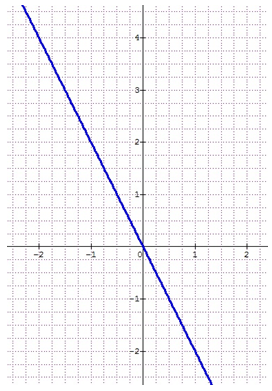
Question 8
La droite ci-contre est la représentation graphique de la fonction \(f\) telle que :
\(f(x) = 2x - 1\)
\(f(x) = 2x + 1\)
\(f(x) = -2x - 1\)
\(f(x) = x - 1\)
La représentation graphique d’une fonction linéaire \(f\) est une droite passant par l’origine du repère, or ici ce n’est pas le cas.
La représentation graphique de la fonction affine \(f\) telle que \(f(x) = ax + b\) est une droite passant par le point d’abscisse 0 et d’ordonnée : « l’ordonnée à l’origine » c’est-à-dire \(b\).
\(b\) est donc égal à \(-1\).
Or, d’après le graphique, et d’après la « méthode des escaliers », \(a = 2\).
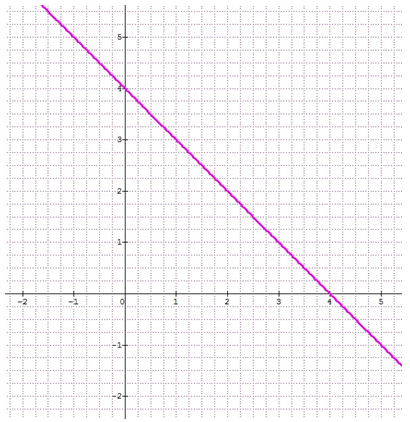
Question 9
La droite ci-contre est la représentation graphique de la fonction \(f\) telle que :
\(f(x) = -4x - 4\)
\(f(x) = -4x + 4\)
\(f(x) = x + 4\)
\(f(x) = -x + 4\)
La représentation graphique d’une fonction linéaire \(f\) est une droite passant par l’origine du repère, or ici ce n’est pas le cas.
La représentation graphique de la fonction affine \(f\) telle que \(f(x) = ax + b\) est une droite passant par le point d’abscisse 0 et d’ordonnée : « l’ordonnée à l’origine » c’est-à-dire \(b\).
b est donc égal à 4.
Or, d’après le graphique, et d’après la « méthode des escaliers », a = -1.
Question 10
La droite passant par l'origine du repère et par le point de coordonnées $(4 ; 16)$ est la représentation graphique de la fonction $f$ :
$f(x)= 2x+4$
$f(x)=x+4$
$f(x)= 4x$