L'énoncé
M. Jean possède un terrain qu’il souhaite partager en deux lots de même aire. Ce terrain a la forme d’un triangle \(ABC\) rectangle en \(A\) tel que \(AB = 50 m\) et \(AC = 80 m\).
Question 1
Calculer l'aire du triangle \(ABC\).
\(A_{ABC} = \dfrac{Base \times Hauteur}{2}\)
\(A_{ABC}= \dfrac{AB \times AC}{2} = \dfrac{50 \times 80}{2} = \dfrac{4 000}{2}\)
\(A_{ABC}= 2 000 \ m^2\)
Aire d’un triangle = \(\dfrac{Base \times Hauteur}{2}\)
Question 2
En déduire que l'aire de chaque lot doit être 1 000 m\(^2\).
M. Jean veut partager son terrain en deux lots de même aire, chaque lot aura donc une aire de \(\dfrac{2 000}{2} = 1 000 m^2\)
Dans le 1)a) vous avez calculé l’aire totale du triangle \(ABC\), or M. Jean veut partager son terrain en 2 lots.
Question 3
Dans un premier temps, il pense faire deux lots ayant la même forme de deux triangles \(AMC\) et \(BMC\) comme indiqué sur la figure.
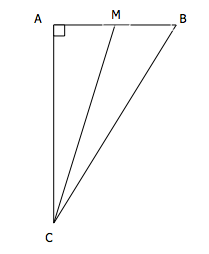
On pose \(AM = x\).
Exprimer en fonction de \(x\) l'aire du triangle \(AMC\).
\(A_{AMC} = \dfrac{Base \times Hauteur}{2}\)
\(A_{AMC}= \dfrac{AM \times AC}{2} = \dfrac{x \times 80}{2}\)
\(A_{AMC}= 40x\)
Pensez à l’aire d’un triangle rectangle.
\(AM\) = base = \(x\) et \(AC\) = hauteur = 80 m.
Question 4
Exprimer en fonction de \(x\) l'aire du triangle \(BMC\).
Première façon :
\(A_{BMC} =\dfrac{Base \times Hauteur}{2}\)
\(A_{BMC}=\dfrac{MB \times AC}{2}=\dfrac{(50-x) \times 80}{2} \)
\(A_{BMC}= (50 - x) \times 40 = 2000-40x\)
Deuxième façon :
\(A_{BMC} = A_{ABC}- A_{AMN} = 2 000 -40x\)
- Soit vous calculez directement l’aire du triangle BMC en utilisant la formule de l’aire d’un triangle rectangle.
- Soit vous considèrez que l’aire du triangle BMC = Aire du triangle ABC – Aire du triangle AMC.
Question 5
Déterminer \(x\) pour que les aires des deux triangles \(AMC\) et \(BMC\) soient égales.
On a donc :\(A_{AMC}=A_{BMC}\)
Ce qui revient à \(40x = 2 000 -40x\), on va donc résoudre cette équation
\(80x = 2 000\)
\(x = \dfrac{2 000}{80}\)
\(x = 25\)
Utilisez les questions précédentes 2)a) et 2)b).
Vous connaissez les expressions des aires des deux triangles, ces deux expressions sont donc égales.
Question 6
Quelle est la position du point \(M\) sur le segment \([AB]\) ?
Si \(x = 25\), cela signifie que \(AM = 25 m\).
Puisque \(M\) est sur le segment \([AB]\) et que \(AB = 50m.\)
Alors \(M\) est le milieu de \([AB]\).
La solution de l’équation précédente vous donne la valeur de \(x\) qui est la distance de \(A\) à \(M\).
Question 7
On considère les deux fonctions affines \(f\) et \(g\) définies par :
\(f(x) = 40x\) et \(g(x) = 2 000 -40x\)
Sur une feuille de papier millimétré, construire un repère orthogonal :
- L'origine sera placée en bas à gauche.
- Sur l'axe des abscisses, on prendra 1 cm pour 5 unités (1 cm pour 5 m)
- Sur l'axe des ordonnées, on prendra 1 cm pour 100 unités (1 cm pour 100 m\(^2\))
Dans ce repère, représenter graphiquement les fonctions affines \(f\) et \(g\) pour \(0 \leq x \leq 50\).
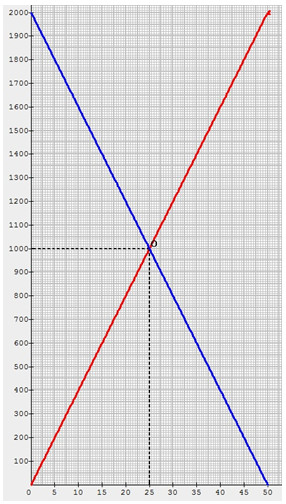
La représentation graphique de la fonction affine (et linéaire) \(f\) telle que \(f(x) = 40x\) est une droite qui passe par l'origine du repère (droite tracée en rouge).
La représentation graphique de la fonction affine \(g\) telle que \(g(x) = 2 000 - 40x\) est une droite qui passe par le point de coordonnées \((0 ; 2 000)\) (droite tracée en bleu).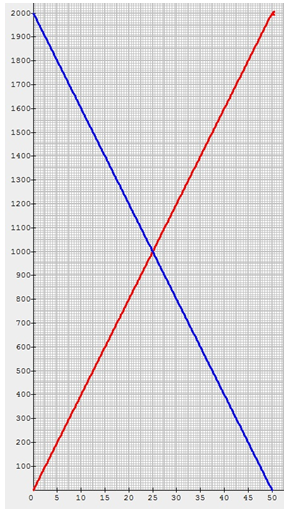 
Si cette fonction affine est une fonction linéaire, la droite passe par l’origine du repère.
Question 8
En utilisant ce graphique, retrouver le résultat de la question 6
M. Jean partage son terrain en deux lots de 1000 m\(^2\).
Les aires de ces deux lots sont égales au point où ces deux droites se coupent. C'est-à-dire pour \(x = 25 m\). 
Il suffit maintenant de lire l’abscisse du point d’intersection.
Question 9
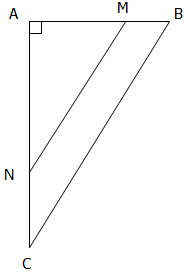
Finalement, Monsieur Jean se décide à partager son terrain en un lot triangulaire \(AMN\) et un lot ayant la forme d'un trapèze \(BMNC\).
(Comme indiqué sur la figure avec \((MN)\) parallèle à \((BC)\)).
On pose \(AM = x\).
En utilisant la propriété de Thalès, exprimer \(AN\) en fonction de \(x\).
Dans le triangle \(ABC\),
- \(M \in [AB]\)
- \(N \in [AC]\)
- Et \((MN)\) est parallèle à \((BC)\)
D'après la propriété de Thalès : \(\dfrac{AN}{AC} = \dfrac{AM}{AB} = \dfrac{MN}{BC}\).
Ainsi : \(\dfrac{AN}{80} = \dfrac{x}{50}\).
Ce qui nous donne : \(AN = \dfrac{80 \times x}{50}\)
\(AN = \dfrac{8}{5} x\)
On peut donc exprimer \(AN\) en fonction de \(x\).
La propriété de Thalès nous donne : \(\dfrac{AN}{AC} = \dfrac{AM}{AB} = \dfrac{MN}{BC}\)
Question 10
En déduire que l'aire du triangle \(AMN\) est égale à \(\dfrac{4}{5} x^2\).
\(A_{AMN} = \dfrac{Base \times Hauteur}{2}\)
\(A_{AMN}= \dfrac{ AM \times AN}{2} = \dfrac{x \times \dfrac{8}{5}x}{2} \)
\(A_{AMN}= \dfrac{4}{5}x^2\)
D’après la question précédente \(AN = \dfrac{8}{5}x\).
Question 11
Le graphique suivant représente l'aire en m\(^2\) du triangle \(AMN\) exprimée en fonction de \(x\).
En utilisant ce graphique, déterminer \(x\), à un mètre près, pour que les aires des deux lots \(AMN\) et \(BMNC\) soient égales.
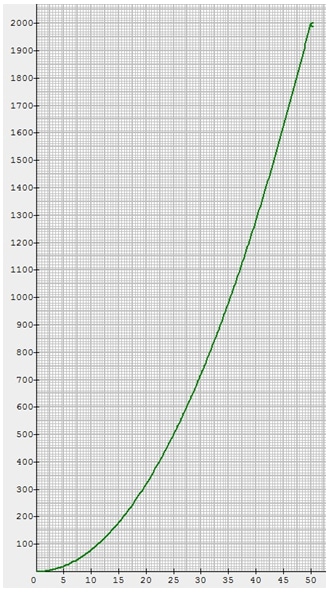
Les deux aires sont égales à 1 000 m\(^2\).
Le graphique donné dans le sujet est la représentation graphique de l'aire du triangle \(AMN\).
Le triangle \(AMN\) doit avoir une aire de 1 000 m\(^2\), \(x\) est donc l'abscisse du point de la courbe d'ordonnée 1 000.
\(x\) est donc environ égal à 35 m\(^2\).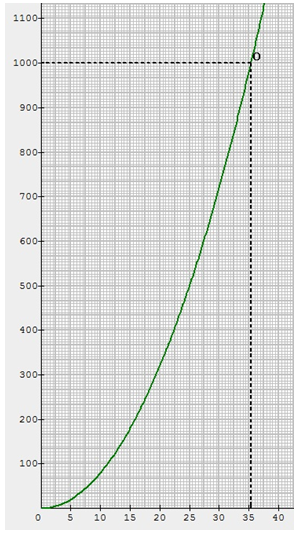
Le terrain fait toujours 2 000 m\(^2\), M. Jean veut le partager en deux lots de même aire, c’est-à-dire de 1 000 m\(^2\) chacun.
Il suffit maintenant de lire l’abscisse du point de la courbe d’ordonnée 1 000.