Prendre une feuille et un crayon et répondre aux questions suivantes.
Partie 1
La distance d’arrêt est la distance qu’il faut pour immobiliser un véhicule sur la plus courte distance possible. Sur le graphique donné ci-dessous, on a représenté les distances d’arrêt en fonction de la vitesse pour une voiture sur route sèche et sur route mouillée.
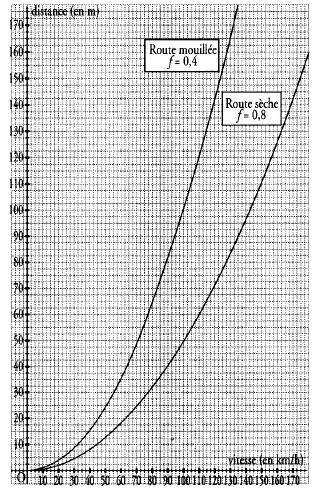
En utilisant ce graphique, répondre aux questions suivantes :
1) La distance d’arrêt est-elle proportionnelle à la vitesse ? Justifier.
2) Une voiture roule sur route sèche.
a) Quelle est la distance d’arrêt lorsqu’on roule à 90 km/h ? (laisser des traces graphiques).
b) A quelle vitesse correspond une distance d’arrêt de 100 m ?
3) Une voiture roule sur route mouillée. Quelle est la distance d’arrêt lorsqu’on roule à 90 km/h ?
4) Recopier et compléter le tableau suivant :
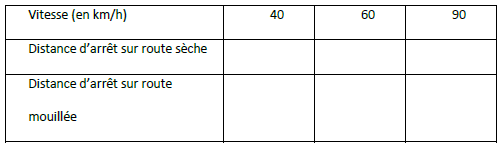
Partie 2
A la lecture de ce tableau, deux quantités semblent proportionnelles. Lesquelles ? Qu’est-ce que cela signifie ?
La distance d’arrêt d’un véhicule peut être calculée par la formule :
$\dfrac{v^{2}}{254 \times f}$
avec : d : distance d’arrêt en mètres, v : vitesse en km/h et f est le coefficient d’adhérence des pneus sur le sol (il dépend de l’état de la chaussée et de la route). Sur route sèche, $f = 0,8$ et sur route mouillée, $f = 0,4$.
1) Il pleut. Une voiture roule sur autoroute à $130$ km/h. Calculer la distance d’arrêt.
2) La route est sèche. Montrer que la vitesse correspondant à une distance d’arrêt de $50$ mètres est d’environ $100$ km/h.
Partie 3
Un conducteur a besoin d’un temps de réaction pour identifier une situation. Pendant ce temps, le véhicule parcourt une certaine distance appelée distance de réaction. Dans des conditions normales, le temps de réaction est de 1 seconde. La distance totale de freinage est la somme de la distance d’arrêt et de la distance de réaction.
1) La route est sèche. Une voiture roule à $90$ km/h. Déterminer la distance du temps de réaction à un mètre près. En déduire la distance totale de freinage.
2) Soit v la vitesse du véhicule en km/h. La distance dR de réaction (en mètres) est donnée par la formule : $d_{R}(v)=\dfrac{5 \times v}{18}$
a) Recopier et compléter le tableau suivant :
b) Représenter dans un repère la fonction d_{R}.
3) Une voiture roule sur autoroute à 130 km/h (la route est sèche). Le conducteur aperçoit n obstacle dans ses phares à 100 m devant lui. Il doit alors faire un freinage d’urgence. Aura-t-il le temps de s’arrêter ? Justifier.
4) Il pleut. Une voiture roule à 90 km/h et le conducteur est fatigué. Son temps de réaction est de 2 secondes. Calculer la distance totale de freinage.
Partie 1
1) Les distances d’arrêt sur routes sèche et mouillée ne sont pas proportionnelles à la vitesse car leur représentation graphique n’est pas une droite passant par l’origine du repère.
2) a) La distance d’arrêt lorsqu’on roule à $90$ km/h sur une route sèche est $40$ m.
b) La vitesse correspondant à une distance d’arrêt de $100$ m sur route sèche est $145$ km/h.
3) La distance d’arrêt lorsqu’on roule à $90$ km/h sur une route mouillée est $80$ m.
4) La distance d’arrêt sur route sèche semble proportionnelle à la distance d’arrêt sur route mouillée car le rapport.de ces deux grandeurs est une constante : 
Distance d’arrêt sur route mouillée / Distance d’arrêt sur route sèche = 2
La distance d’arrêt sur route mouillée est le double de celle sur route sèche.
Partie 2
1) d=$\dfrac{v^{2}}{254 \times f}$ soit $d=\dfrac{130^{2}}{254 \times 0.4} = 166.3$
2) $50$=$\dfrac{v^{2}}{254 \times 0.8}$ soit $v^{2}$=$50 \times 254 \times 0.8$ = $10160$
$v$= $\sqrt{10160}$=$100.8 $ km/h
La vitesse correspondant à une distance d’arrêt de 50 m sur route sèche est bien environ 100 km/h.
Partie 3
1) a) $d=v \times t$
Comme v est en km/h, je convertis le temps de réaction (1 s) en heure : $1 s =\dfrac{1}{3600} $h.
$d$=$90 \times \dfrac{1}{3600}$=$0.025$km=$25$m
La distance de réaction, sur route sèche, pour une voiture roulant à $90$ km/h est $25$ m distance totale de freinage = distance de réaction + distance d’arrêt distance totale de freinage = $25 + 40 = 65$ distance totale de freinage = $65$ m
La distance totale de freinage à 90 km/h sur route sèche est $65$ m
2) a)
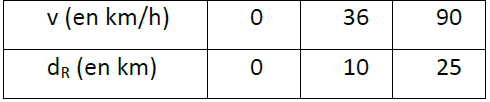
b) Le conducteur ne peut pas s’arrêter avant l’obstacle.
3) Voir graphique. Soient :
• da la distance d’arrêt
• df la distance totale de freinage
• dr la distance de réaction $df = d_{R} + d_{a}$
D’après le graphique : $d_{f} = 35 + 80 = 115 $
Donc : $d_{f} = 115 $ m
4) $d_{f} = d_{R} + d_{a}$
Calcul de la distance parcourue pendant un temps de réaction de 2 s
$d_{R}(v)$=$2 \times \dfrac{5 \times v}{18}$
$d_{R}(v)$=$2 \times \dfrac{5 \times 90}{18}=50$ m
La distance d’arrêt sur route mouillée à déjà été déterminée graphiquement partie I question 4).
On a $d_{a}$ = $80$ m Donc $d_{f}$ = $50 + 80$ = $130$ ; Donc $d_{f}=130$ m
La distance totale de freinage est 130m.
