L'énoncé
Question 1
\(|z-3|=|z-3i|\)
Dans le plan muni du repère orthonormal \((O;\overrightarrow{u} ;\overrightarrow{v} )\).
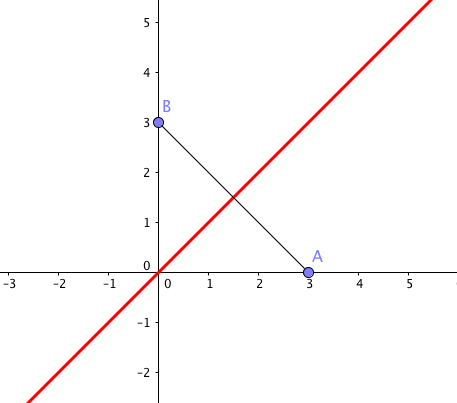
On note \(A\) et \(B\) les points dont les affixes respectives sont \(3\) et \(3i\), et \(M\) le point dont l'affixe est notée \(z\).
Par définition \(|z-z_A| = AM\) si \(z\) et \(z_A\) sont les affixes respectifs de \(M\) et \(A\).
L'égalité \(|z-3|=|z-3i|\) se traduit par \(AM=BM\) .
Le point \(M\) étant équidistant des points \(A\) et \(B\), il appartient à la médiatrice de \([AB]\). La réciproque est vraie.
L'ensemble des points \(M\) du plan dont l'affixe \(z\) vérifie \(|z-3|=|z-3i|\) est donc la médiatrice de \([AB]\), avec \(A(3)\) et \(B(3i)\).
Par définition \(|z-z_A| = AM\) si \(z\) et \(z_A\) sont les affixes respectifs de \(M\) et \(A\).
Cette équation doit se traduire par une égalité de deux longueurs.
Faites une figure pour chercher l’ensemble des points \(M\)
Question 2
\(|2-3i+z|=|2+3i|\)
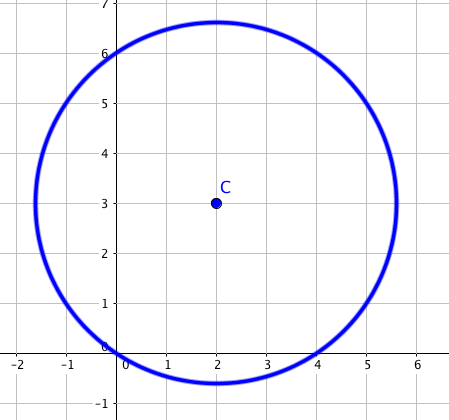
Notons \(C\) le point dont l'affixe est \(2+3i\).
Puisque \(|2+3i|=\sqrt{2^2+3^2}=\sqrt{13}\),
L'égalité \(|2-3i+z|=|2+3i| \Leftrightarrow |z-(-2+3i)|=\sqrt{13}\) se traduit par :
\(CM=\sqrt{13}\)
Le point \(M\) appartient donc au cercle de centre \(C\) et de rayon \(\sqrt{13}\). La réciproque est vraie.
L'ensemble des points \(M\) du plan dont l'affixe \(z\) vérifie \(|2-3i+z|=|2+3i|\) est donc le cercle de centre \(C(2+3i)\) et de rayon \(\sqrt{13}\).
On doit en revanche trouver ici une longueur égale à un réel positif.
Une figure vous aidera encore certainement.
Question 3
\(|\overline{z}-4+i|=1\)
1ère méthode :
Si on pose \(z=x+iy\), avec \(x,y \in \mathbb{R}\), l'égalité \(|\overline{z}-4+i|=1\) est équivalente à :
\(|\overline{z}-4+i|^2=1^2=1\)
\(\Leftrightarrow |x-iy-4+i|^2=1 \)
\(\Leftrightarrow |x-4-i(y-1)|^2=1 \)
\(\Leftrightarrow (x-4)^2+(y-1)^2=1\)
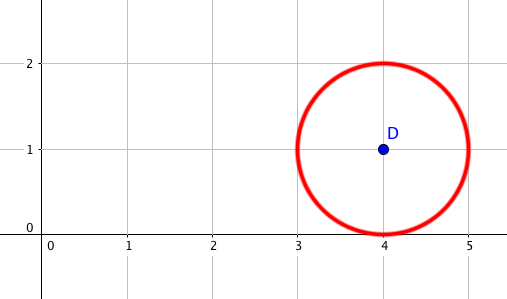
On reconnaît là l'équation du cercle de centre \(D(4 +i)\) et de rayon 1.
2ème méthode :
\(|z|=|\overline{z}|\) donc on a :
\(|\overline{z}-4+i|=\overline{|\overline{z}-4+i}|\)
\(\Leftrightarrow|\overline{z}-4+i|=|z-4-i|\)
\(\Leftrightarrow|\overline{z}-4+i|=|z-(4+i)|\)
\(\Leftrightarrow|\overline{z}-4+i|=|z-z_D|\)
Ainsi : \(|z-z_D|=1\) avec \(z_D =4+i\)
L'ensemble des points \(M\) du plan dont l'affixe \(z\) vérifie \(|\overline{z}-4+i|=1\) est donc le cercle de centre \(D(4+i)\) et de rayon 1.
Ici, c’est le conjugué de \(z\) qui apparait. Il peut s’avérer utile de poser \(z = x+iy\).
Séparer la partie réelle et la partie imaginaire pour le calcul du module.
Vous devez obtenir une équation du second degré bien connue.
2ème méthode :
\(|z|=|\overline{z}|\) et \(\overline{z}=z\) donc \(|\overline{z}-4+i|=|\overline{\overline{z}-4+i}|=|z-4-i|\)
Question 4
\(arg(\overline{z}) = arg(-z) +2k\pi \\k \in \mathbb{R}\)
Puisque pour tout complexe \(z\) non nul, on a:
\(arg(\overline{z}) = -arg(z) (2\pi )\) et
\(arg(-z) = arg(z)+ \pi (2\pi )\)
L'égalité : \(arg(\overline{z}) = arg(-z) (2\pi)\) se réécrit :
\(-arg(z) = arg(z)+ \pi (2\pi )\)
Soit \(arg(z)=-\dfrac{\pi}{2}(\pi)\)
L'ensemble des points \(M\) du plan dont l'affixe \(z\) vérifie \(arg(\overline{z}) = arg(-z) (2\pi)\) est donc l'axe des imaginaires purs, privé de l'origine O.
