Fiche de cours
Caractérisations des nombres complexes
Réels et imaginaires purs
Soit $z=a+ib$ un nombre complexe quelconque.
On dit que $z$ est réel lorsque $b=0$ et que $z$ est imaginaire pur lorsque $a=0$.
Exemple
- $2i$ est imaginaire pur,
- $3$ est réel
- $3+2i$ n'est ni réel, ni imaginaire pur.
Caractérisation avec les parties réelles et imaginaires
On constate simplement que si $z$ est un nombre complexe non nul, $\boxed{z\in \mathbb{R} \Leftrightarrow Im(z)=0}$.
Autrement dit, $z$ est réel si et seulement si sa partie imaginaire est nulle.
De même, $z$ est imaginaire pur si et seulement si sa partie réelle est nulle : $\boxed{z\in i\mathbb{R} \Leftrightarrow Re(z)=0}$.
Caractérisation avec l'argument
Soit $z$ un nombre complexe non nul.
$\bullet$ $z$ est réel si et seulement si $arg(z)=k\pi$ avec $k\in \mathbb{Z}$.
$\bullet$ $z$ est imaginaire pur si et seulement si $arg(z)=\dfrac{\pi}{2}+k\pi$ avec $k\in \mathbb{Z}$.
Illustration graphique
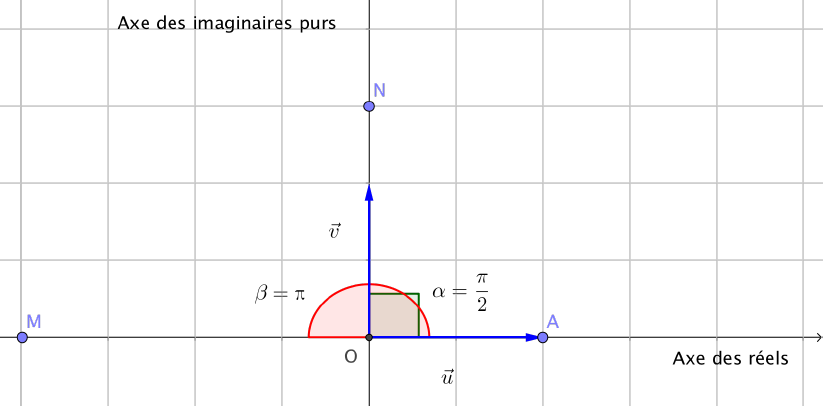
L'affixe du point $M$ est un réel négatif, ta
