Fiche de cours
Nombres complexes et vecteurs
Distances et vecteurs
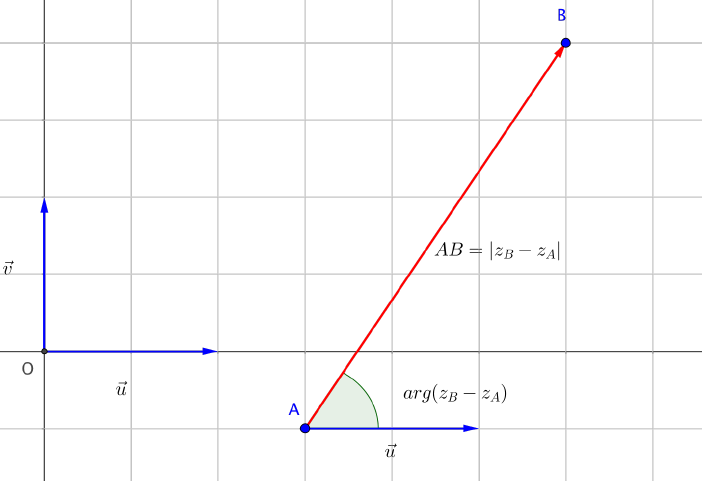
On considére deux points $A$($z_A$) et $B$($z_B$) du plan complexe $\left(O;\overrightarrow{u};\overrightarrow{v}\right)$.
Le milieu $I$ du segment $[AB]$ a pour affixe :
$z_I=\dfrac{z_A+z_B}{2}$.
Le vecteur $\overrightarrow{AB}$ a pour affixe $z_B-z_A$.
Il en résulte donc que la distance $AB$ vaut :
$AB=|z_B-z_A|$.
Angles et arguments
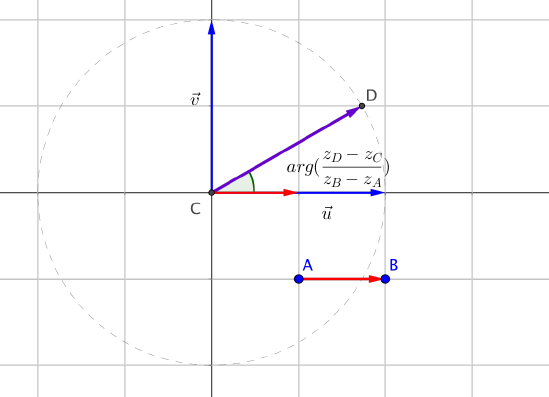
Soient $A(z_A)$, $B(z_B)$, $C(z_C)$ et $D(z_D)$ quatre points du plan complexe $\left(O;\overrightarrow{u};\overrightarrow{v}\right)$.
On a les résultats suivants :
$ \boxed{ arg(z_B-z_A)=(\overrightarrow{u},\overrightarrow{AB}) ~ [2\pi]}$
$\boxed{ arg\bigg(\dfrac{z_D-z_C}{z_B-z_A}\bigg) = (\overrightarrow{AB},\overrightarrow{CD}) ~ [2\pi]}$
Exemple
On donne les quatre points suivants :
$A(0,0)$, $B(\dfrac{\sqrt3}{2},\dfrac12)$, $C(\dfrac12,-\dfrac12)$ et $D(1,-\dfrac12)$.
Calculer une mesure de l'angle $(\overrightarrow{AB},\overrightarrow{CD})$.
On commence par do
