Fiche de cours
Module et argument
Module
On considère un nombre complexe $z=a+ib$ et on note $M$ le point du plan complexe d'affixe $z$.
On définit le module de $z$ (qu'on note $|z|$) par la distance du point $M$ au point d'origine $O$.
On a alors la formule suivante :
$|z|=OM =\sqrt{a^2+b^2}$
Argument
On note $\overrightarrow{u}$ le vecteur directeur de norme $1$ de l'axe des réels.
On définit alors l'argument d'un nombre complexe $z=a+ib$ (affixe du point $M$ dans le plan complexe) l'angle formé par le vecteur $\overrightarrow{u}$ et le vecteur $\overrightarrow{OM}$.
On écrit alors :
$ \operatorname{arg} (z) = (\overrightarrow{u}, \overrightarrow{OM} ) ~ [2\pi]$
En notant $\theta = \operatorname{arg}(z)~ [2\pi]$ alors on a les égalités suivantes :
- $\cos(\theta)=\dfrac{a}{|z|}$
- $\sin(\theta)=\dfrac{b}{|z|}$
Illustration graphique
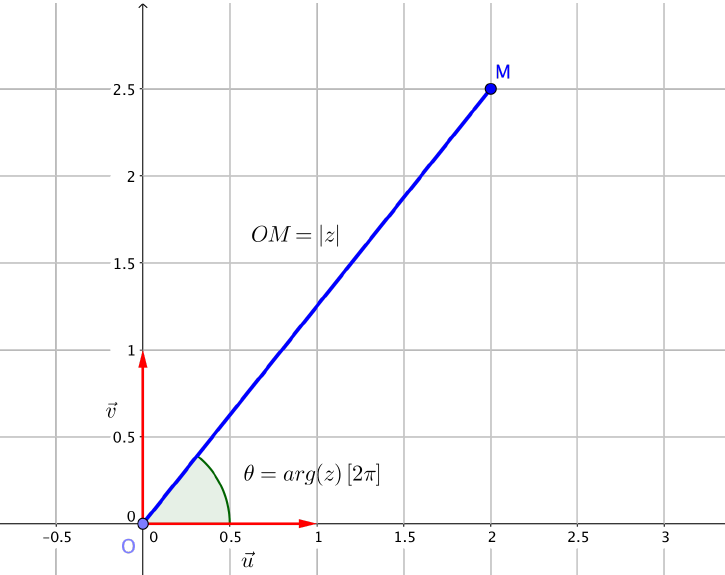
L'angle $\theta$ est ici un argument de $z$ : $\operatorname{arg}(z)=\theta ~ [2\pi]$.
Exemple
Calculer le module et un argument de $z_1=1+i$ et $z_2=4-4i$.
$z_1$ s'Ècrit : $z_1=a_1+ib_1$ avec
