Fiche de cours
Egalité de complexes, conjugués, opérations élémentaires
Egalité de nombres complexes
On dit que deux nombres complexes $z=a+ib$ et $z'=a'+ib'$ sont égaux si et seulement si $a=a'$ et $b=b'$.
Opérations élémentaires
Les opérations de sommes, différences, multiplications et divisions existent dans $\mathbb{C}$.
Pour $z=a+ib$ et $z'=a'+ib'$ deux nombres complexes alors :
$\bullet$ $z+z' = (a+a')+i (b+b')$
$\bullet$ $z\cdot z' = (a+ib)\cdot (a'+ib') = (aa'-bb') + i (a'b+ab')$
Conjugué d'un nombre complexe
On considère un nombre complexe quelconque $z=a+ib$ avec $a\in \mathbb{R}$ et $b\in\mathbb{R}$.
On appelle conjugué de $z$ et on note $\bar z$ le nombre $a-ib$.
Exemple : si $z=1,5+i$ alors $\bar z = 1,5-i$.
Illustration graphique
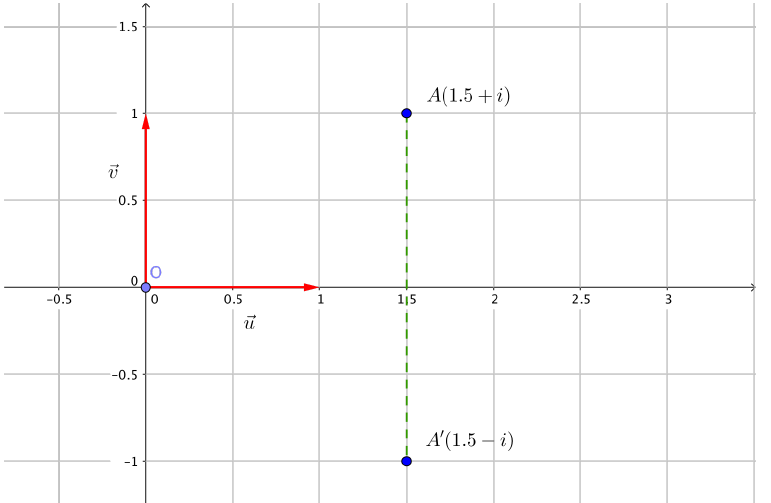
Le point $A'$ d'affixe $\bar z$ est le symétrique du point $A$ d'affixe $z$ par rapport à l'axe des abscisses
Propriétés des conjugués
si $z$ et $z'$ sont deux nombres complexes (avec $z'$ non nul), alors :
$\bullet $ $\overline{z+z'} = \bar z + \bar{z'}$
$\bullet $ $\overline{zz'} = \bar z \cdot \bar z'$
$\bullet$ $\overline{\left(\dfrac{z}{z'}\right)} = \dfrac{\bar z}{\bar{z'}}$
