Fiche de cours
Définition des nombres complexes
L'ensemble $\mathbb{C}$
Un nombre complexe $z$ se présente sous la forme $z=a+i b$ où $a$ et $b$ sont réels et $i$ est tel que $i^2=-1$.
On appelle $a$ la partie réelle de $z$ et on note : $\mathcal{Re}(z)=a$.
On appelle $b$ la partie imaginaire de $z$ et on note : $\mathcal{Im}(z)=b$.
On note alors $\mathbb{C}$ l'ensemble des nombres complexes : $$ \mathbb{C}= \{a+ib ~|~ a,b\in \mathbb{R}\} $$
Illustration graphique
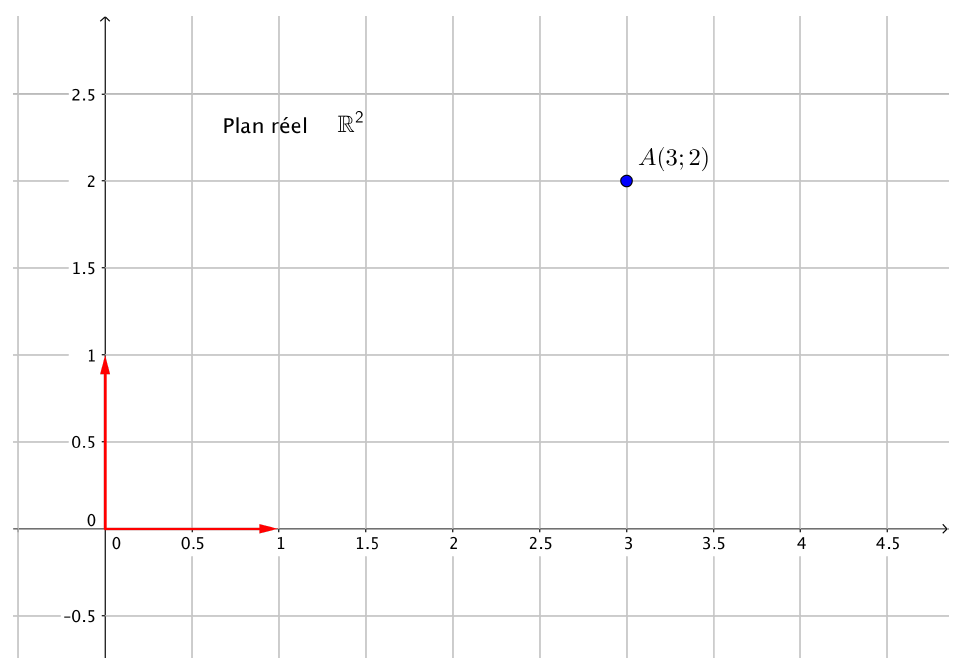
Plan réel :
Plan complexe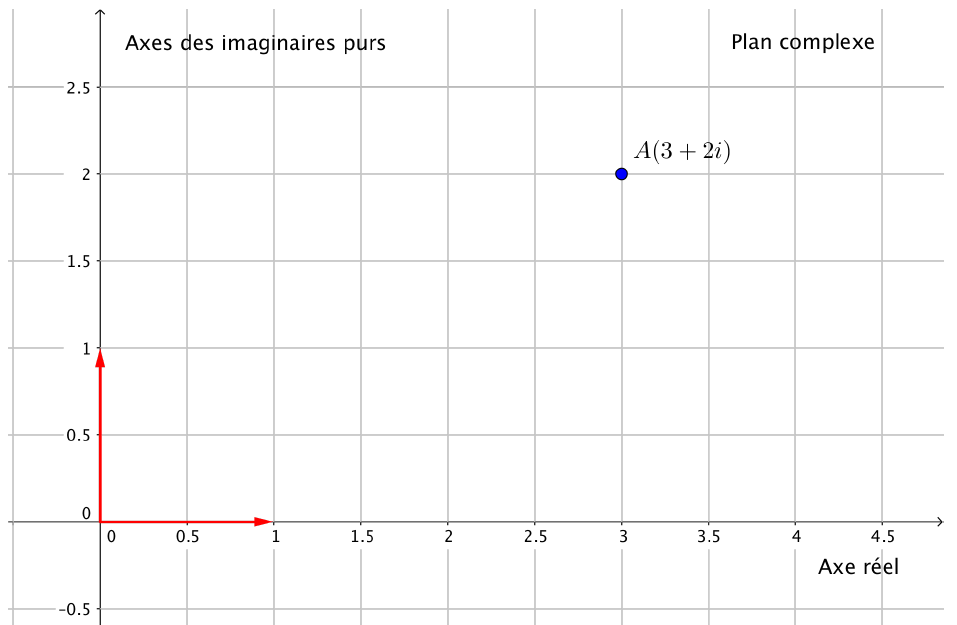
Le point $A$ est représenté par le nombre complexe $z=3+2i$ dans le plan complexe.
On parle d'affixe dans le plan complexe et de coordonnées dans le plan réel.
On dit que $z$ est l'affixe du point $A$ et on note $A(3+2i)$
