L'énoncé
Soit \(g\) la fonction définie sur \([1 ; 10]\) par \(g(x)= \dfrac{5}{(x+1)}\).
Question 1
Calculer la dérivée de \(g\).
\(g'(x) = - \dfrac{5}{(x+1)^2}\)
Savez-vous dériver \(g\) ? Sinon regardez la vidéo.
Question 2
Quel est le sens de variation de \(g\) sur \([1 ; 10]\) ?
Pour tout \(x\) dans \([1 ; 10]\), \(g'\) est négative donc \(g\) est décroissante.
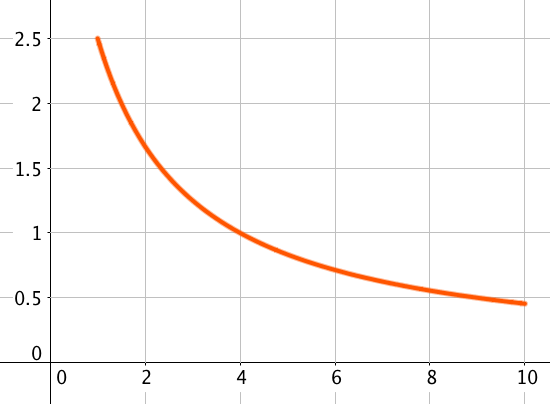
Quel est le signe de \(g’\) ? Ainsi \(g\) est…
Question 3
Quel est le sens de variation de \(g'\) ?
\(g''(x)= \dfrac{10(x+1)}{(x+1)^4} = \dfrac{10}{(x+1)^3}\)
\(x\) appartient à \([1 ; 10]\) donc \(g''(x)\) est positive pour tout \(x\) de \([1 ; 10]\).
Ainsi \(g'\) est croissante.
Avez-vous pensé à dériver \(g’\) ? Le signe de \(g’’\) donnera le sens de variation de \(g’\).
Question 4
La fonction \(g\) est-elle convexe ? Concave ?
« Une fonction \(g\) est convexe sur un intervalle \(I\) si et seulement si sa dérivée est croissante sur \(I\). »
La fonction \(g'\) étant croissante, elle est convexe sur \([1 ; 10]\).
Connaissez-vous le théorème majeur sur les fonctions convexes ?
« Une fonction \(g\) est convexe sur un intervalle \(I\) si et seulement si sa dérivée est … sur \(I\). »
