L'énoncé
Une entreprise fabrique des vases. Le bénéfice, en centaine d’euros, réalisé par la production et la vente de \(x\) centaines de vases est modélisé par la fonction suivante :
\(B(x) = -3x^2 +33x - 54\) pour \( 1 \leq x \leq 10\).
Question 1
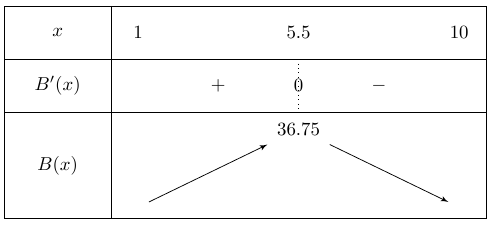
Étudier les variations de \(B\) sur \([1 ; 10]\).
\(B\) est dérivable sur \([1 ; 10]\) et
\(B'(x) = -6x +33.\)
\(-6x +33 \geq 0 \Leftrightarrow x \leq 5,5\)
Avez-vous pensé à dériver \(B\) ? Il suffit d’étudier le signe de la dérivée !
Question 2
Quel nombre de vases faut-il produire et vendre pour réaliser un bénéfice maximum ? Donner la valeur de ce bénéfice.
\(B\) admet un maximum pour \(x=5,5\). Il faut donc produire et vendre 550 vases pour réaliser un bénéfice maximum.
\(B(5,5) = -3 \times 5,5^2 +33 \times 5,5 -54\)
\(B(5,5) = 90,75 + 181,5 - 54\)
\(B(5,5) = 36,75\)
Le bénéfice est alors de 3 675 € .
Le tableau de variation de \(B\) donne la solution… La fonction admet un maximum en \(x\) =…
Question 3
Résoudre l'équation \(B(x)=0\). Interpréter économiquement ce résultat.
\(B(x) = 0 \)
\(\Leftrightarrow -3(x^2-11x+18) = 0\)
\(\Leftrightarrow -3(x-9)(x-2) = 0\)
\(S = \{2 ; 9\}\)
Pour 200 et 900 vases, le bénéfice est nul.
200 et 900 sont appelés les points morts de la production.
Avez-vous réussi à factoriser \(B\) ? Commencez par factoriser par \(-3\), cela aidera à trouver les racines. Si vous ne voyez pas de racine évidente, calculez le déterminant.
Savez-vous ce qu’est un point mort ?
Question 4
Résoudre l'inéquation \(B(x) \geq 0\). En déduire la plage de bénéfice de la production.
\(B(x) \geq 0 \)
\(\Leftrightarrow -3(x^2-11x+18) \geq 0\)
\( \Leftrightarrow(x-9)(x-2)\leq 0\)
\(S = [2 ; 9]\)
La plage de bénéfice de la production se situe entre 200 et 900 vases.
Utiliser la factorisation trouvée à la question précédente. La plage de bénéfice d’une production est l’intervalle pour lequel le bénéfice est positif.
