Partie A

On considère une fonction $g$ définie sur l’intervalle $\left]-\dfrac{1}{2};+\infty\right[$ par:

$g(x)=-x^2+ax-\ln(2x+b)$ où $a$ et $b$ sont deux réels.

Calculer $a$ et $b$ pour que la courbe représentative de $g$ dans un plan d’un repère $(O; I, J)$ passe par l’origine du repère et admette une tangente parallèle à l’axe des abscisses au point d’abscisse $\dfrac{1}{2}$. 

Partie B

Soit $f$ la fonction définie sur l’intervalle $\left]-\dfrac{1}{2};+\infty\right[$ par :

$f(x)=-x^2+2x-\ln(2x+1)$

On admet que $f$ est dérivable et on note $f'$  sa dérivée.

Le tableau de variation de la fonction $f$ est le suivant :

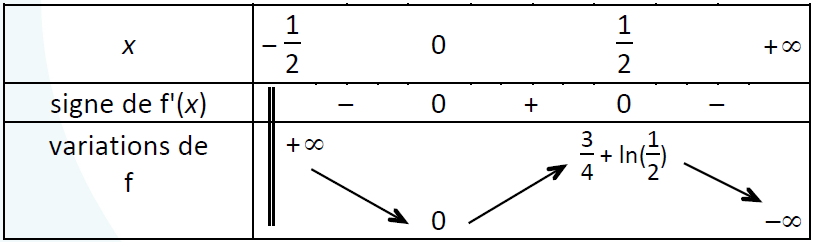
1) Justifier tous les éléments contenus dans ce tableau.

2) a) Montrer que l’équation $f(x) = 0$ admet une unique solution $\alpha$ dans l’intervalle $\left[\dfrac{1}{2};1\right]$.

b) Donner un encadrement de $\alpha$ d’amplitude $10^{-2}$.

3) Déterminer le signe de $f(x)$ sur l’intervalle $\left]-\dfrac{1}{2};+\infty\right[$.