L'énoncé
Pour tout entier \(n\) supérieur ou égal à $1$, on considère la fonction \(f_n\) définie sur \([0;1]\) par : \(f_n(x)=x^n e^{-x}\)
On note \(C_n\) sa représentation graphique dans un repère orthonormé.
On désigne par \((I_n)\) la suite définie pour tout entier \(n\) supérieur ou égal à $1$ par :
\(I_n= \displaystyle \int_0^1 x^n e^{-x} \, dx\)
On admet que \(I_1 = -2e^{-1}+1\).
Question 1
Dans cette question, toute trace de recherche ou d'intiative, même incomplète, sera prise en compte dans l'évaluation.
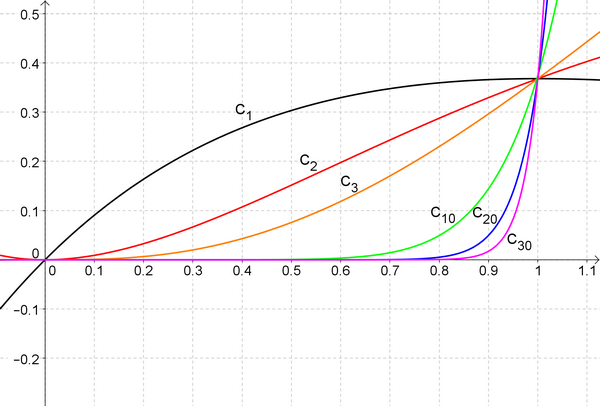
Sur le graphique ci-dessous, on a représenté les portions des courbes \(C_1,\,C_2,\,C_3,\,C_{10},\,C_{20},\,C_{30}\) avec \(0 \leq x \leq 1\).
Formuler une conjecture sur le sens de variation de la suite \((I_n)\) en décrivant la démarche.
Pour tout entier naturel non nul \(n\), \(f_n\) est positive sur [0;1].
Par définition d'une intégrale, on peut donc interpréter géométriquement \(I_n\) comme l'aire délimitée par la courbe \(C_n\), l'axe des abscisses et les droites d'équations \(x=0\) et \(x=1\).
Les représentations données permettent de conjecturer que cette suite d'aires diminue lorsque \(n\) augmente et donc que la suite (\(I_n\)) est décroissante.
Pensez à utiliser l’interprétation géométrique de la notion d’intégrale.
Mettez cette interprétation en correspondance avec le graphique proposé.
Question 2
Démontrer cette conjecture.
Soit \(n\) un entier naturel non nul.
\(I_{n+1}-I_n=\displaystyle \int_0^1 x^{n+1}e^{-x}dx-\displaystyle \int_0^1 x^ne^{-x}dx\)
\(I_{n+1}-I_n=\displaystyle \int_0^1 x^ne^{-x}(x-1)dx\)
Sur l'intervalle [0;1], on a : $x-1\leq 0$ donc \(x^ne^{-x}(x-1) \leq 0\)
On en déduit que \(I_{n+1}-I_n \leq 0\)
Ce qui démontre que la suite \((I_n)\) est décroissante.
Pour étudier le sens de variation d’une suite, pensez qu’il faut étudier le signe de la différence entre deux termes.
Pensez à utiliser les propriétés de l’intégrale : ici on utilise la linéarité
\(\displaystyle \int_a^b(f(x)+g(x))dx=\int_a^b f(x)dx+\int_a^b g(x)dx\) (additivité)
\(\displaystyle \int_a^b \lambda f(x)dx=\lambda \int_a^b f(x)dx\) (homogénéité)
Et la positivité de l'intégrale :
si \(a < b\) et pour tout réel \(x\) de \([a ; b]\) \(f(x) \geq 0\) alors
\(\displaystyle \int_a^b f(x)dx \geq 0\)
Pensez à factoriser par \(x^n\) dans la partie à intégrer. Cela vous permettra d’étudier le signe de la fonction sous le signe intégral.
Il ne faut pas oublier que \(I_n\) est définie sur \([0,1]\) pour l’étude du signe.
Pour l’&ea
Question 3
En déduire que la suite \((I_n)\) est convergente.
Pour tout entier naturel \(n\) non nul et tout réel \(x\) de [0;1], \(f_n(x) \geq 0\), donc par positivité de l'intégrale, pour tout entier naturel \(n\) non nul \(I_n\geq 0\).
La suite \((I_n)\) est décroissante, minorée par $0$ elle est donc convergente.
Penser que toute suite décroissante et minorée converge.
Il faut trouver un minorant pour \(I_n\).
Que peut-on dire du signe de la fonction à intégrer ? Cela devrait permettre de trouver un minorant.
Voit-on des courbes sous l’axe des abscisses ? Comment peut-on l’interpréter ?
Question 4
Déterminer \(\displaystyle\lim_{n \to +\infty} I_n\).
Sur $[0;1]$, on a
\(\dfrac{1}{e}\leq e^{-x}\leq 1\)
Donc \(0 \leq x^ne^{-x} \leq x^n\)
Par passage à l'intégrale sur $[0;1]$ :
\( 0 \leq I_n \leq \displaystyle \int_0^1 x^n dx\)
Donc :
\(0\leq I_n \leq \left[\dfrac{1}{n+1}x^{n+1}\right]_0^1\)
Ainsi : \(0 \leq I_n \leq \dfrac{1}{n+1}\)
Comme \(\displaystyle\lim_{n \to +\infty} \dfrac{1}{n+1}=0\), le théorème des gendarmes nous permet de conclure que :
\(\displaystyle\lim_{n \to +\infty} I_n =0\)
Pensez que sur \([0,1]\), l’exponentielle de \(–x\) est un nombre plus petit que $1$.
Il faut en déduire un encadrement de \(I_n\).
Quel théorème de convergence des suites utilise un encadrement ? Il peut servir ici.