Valeur moyenne d'une fonction

Valeur moyenne d'une fonction

Définition

Soient $a$ et $b$ deux réels tels que $a < b$ et \(f\) est continue sur \([a,b]\).

On appelle valeur moyenne de \(f\) sur \([a,b]\), le nombre réel $\mu$ défini par :

\( \displaystyle \mu = \frac{1}{b-a} \int_{a}^b f(t)dt\)

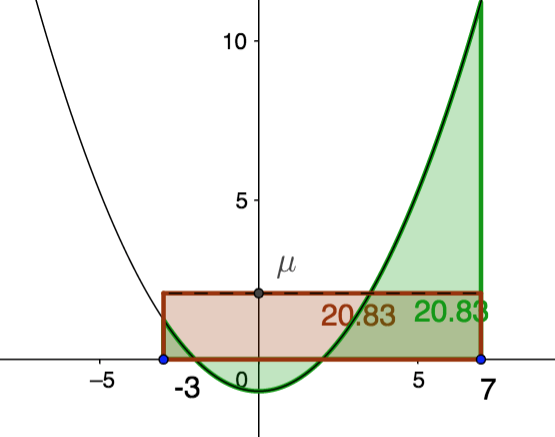
Interprétation graphique

On peut déterminer la valeur de l'intégrale de $f$ en effectuant le produit en croix:

\( \displaystyle \mu (b-a)= \int_{a}^b f(t)dt = \mathcal{A}\)

Voici l'exemple de la fonction $f(x)=0,25x^2-1$ sur l'intervalle $[-3;7]$