L'énoncé
Pour chacune des figures suivante, coche la ou les bonne(s) réponse(s).
Tu as obtenu le score de
Question 1
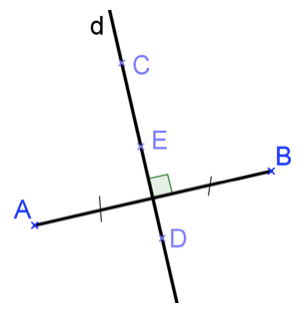
\((AB)\) est la médiatrice de la droite \((CE)\).
\([AB]\) est la médiatrice de la droite \((CD)\).
\(d\) est la médiatrice du segment \([AB]\).
\((CE)\) est la médiatrice du segment \([AB]\).
Qu’est-ce qu’une médiatrice ?
« La médiatrice d’un segment ». Deux propositions peuvent être éliminées…
Un segment se note entre crochets !
« La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu ».
Que signifient les codages de cette figure ?
Il peut y avoir plusieurs bonnes réponses.
Il s’agit de la médiatrice d’un segment donc les propositions 1 et 2 ne peuvent être correctes. La droite \(d\) et la droite \((CE)\) sont confondues donc les propositions 3 et 4 sont les mêmes.
Question 2
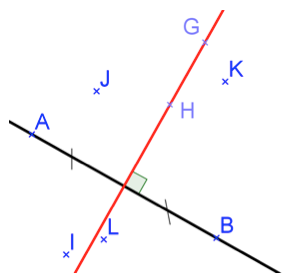
\((AB)\) est la médiatrice de \((ED)\).
\((AB)\) est la médiatrice de \([CF]\).
\((ED)\) est la médiatrice de \([AB]\).
\((ED)\) est la médiatrice de \((AB)\).
Une médiatrice est la médiatrice d’un segment.
Et un segment se note entre … ?
Entre crochets !
Observe les deux autres propositions et les codages de la figure.
Une médiatrice est la médiatrice d’un segment donc les propositions 1 et 4 sont fausses. D’après les codages :
• \((AB)\) est perpendiculaire à \([GF]\) en son milieu donc la proposition 2 est vraie.
• \((ED)\) est perpendiculaire à \([AB]\) en son milieu donc la proposition 3 est vraie.
Question 3
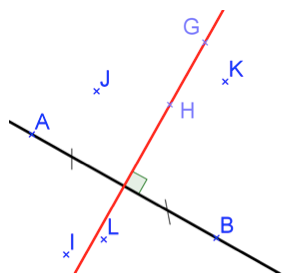
\(D\) est équidistant de \(A\) et de \(B\).
\(G\) est équidistant de \(A\) et de \(B\).
\(C\) est équidistant de \(H\) et de \(F\).
\(C\) est équidistant de \(A\) et de \(B\).
Souviens-toi du cours. Si un point appartient à la médiatrice d’un segment alors … ?
Alors il est équidistant des extrémités de ce segment.
Quels points appartiennent à la médiatrice de \([AB]\) ?
Donc ils sont équidistants de \(A\) et de \(B\). Lis bien les propositions.
On ne connait pas la médiatrice de \([HF]\) !
\(C\) et \(G\) sont deux points de la médiatrice de \([AB]\) donc, par propriété, \(C\) et \(G\) sont équidistants de \(A\) et de \(B\) (mais pas de \(H\) et de \(F\) !) donc les propositions 2 et 4 sont vraies (mais pas la 3).
De plus \(D\) n’appartient pas à la médiatrice de \([AB]\) donc il n’est pas équidistant de \(A\) et de \(B\), (la proposition 1 est fausse).
Question 4
\((AB)\) est la médiatrice de \((GH)\).
\((AB)\) est la médiatrice de \([HG]\).
\((GH)\) est la médiatrice de \([AB]\).
\((HL)\) est la médiatrice de \([AB]\).
Une médiatrice est une médiatrice d’un segment.
Souviens-toi de la définition de la médiatrice d’un segment.
Lis bien les codages de la figure.
Une médiatrice est une médiatrice d’un segment (donc la proposition 1 est fausse).
La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu (donc la proposition 2 est fausse).
\((GH)\) est la droite rouge, c’est à dire la médiatrice de \([AB]\) d’après les codages, donc la proposition 3 est vraie.
Le point \(L\) n’appartient pas à la droite rouge (donc la proposition 4 est fausse).
Question 5
Le point \(K\) est équidistant de \(A\) et de \(B\).
Le point \(K\) est plus proche de \(B\) que de \(A\).
Le point \(K\) est plus proche de \(A\) que de \(B\).
Le point \(G\) est équidistant de \(A\) et de \(B\).
La droite rouge est la médiatrice de \([AB]\) d’après les codages.
Les points de la médiatrice du segment \([AB]\) sont les points qui sont … ?
Équidistants de \(A\) et de \(B\).
\(K\) appartient-il à la droite rouge ? Et \(G\) ?
D’après les codages \((GH)\) est la médiatrice de \([AB]\). \(K\) n’appartient pas à \((GH)\) donc \(K\) n’est pas équidistant de \(A\) et de \(B\) (proposition 1 fausse).
\(K\) est du même côté de la droite \((GH)\) que \(B\) donc \(K\) est plus proche de \(B\) que de \(A\) (proposition 2 vraie et proposition 3 fausse).
\(G\) appartient à la médiatrice \((GH)\) de \([AB]\). Or si un point appartient à la médiatrice d’un segment alors ce point est équidistant des extrémités de ce segment donc \(G\) est équidistant de \(A\) et de \(B\) (proposition 4 vraie).