Cours Droites et médiatrices
lesbonsprofs.com
Image
Cours Droites et médiatrices
1
Video Parallèles et perpendiculaires
2
Exercice QCM - Parallèles et perpendiculaires : applications du cours
3
Exercice QCM - Parallèles et perpendiculaires : applications du cours
4
Exercice QCM - Les droites
5
Video La médiatrice d'un segment
6
Exercice QCM - Médiatrices : applications du cours
7
Exercice Exercice - Construction géométrique et démonstrations

Exercice - Construction géométrique et démonstrations

L'énoncé

Il s’agit d’un seul et même exercice et donc d’une même figure à compléter au fur et à mesure des questions.

Question 1

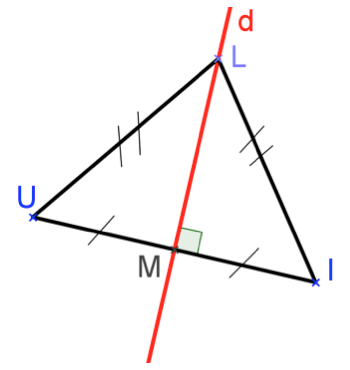
Construis un segment \([UI]\) de 8 cm. Et construis sa médiatrice \(d\).
Souviens-toi de la définition de la médiatrice d’un segment.
Tu dois commencer par construire le milieu de \([UI]\).
Tu dois utiliser l’équerre pour construire la perpendiculaire à \([UI]\) en son milieu.

Question 2

Place un point \(L\) sur \(d\). Quelle est la nature du triangle \(LUI\) ? Démontre-le.
On sait que le point \(L\) appartient à \(d\), la médiatrice de \([UI]\).
Or si un point appartient à la médiatrice dun segment alors il est équidistant des extrémités de ce segment.
Donc \(LU=LI\).
Et donc, par définition, \(LUI\) est un triangle isocèle en \(L\).
« Démontre-le » signifie que tu dois suivre les trois étapes :
On sait que… (données)
Or… (propriété)
Donc… (conclusion)
Que peux-tu dire du point \(L\) ?
\(L\) appartient à la médiatrice du segment \([UI]\) donc \(L\) est… ?
\(L\) est équidistant de \(U\) et de \(I\) !
\(LU=LI\) donc le triangle \(LUI\) est … ?

Question 3

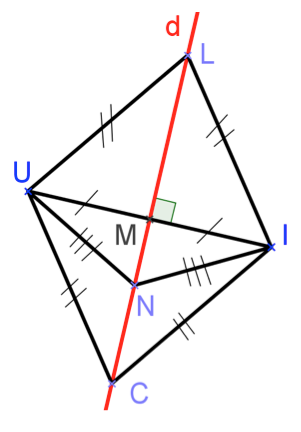
Construis un point \(N\) tel que \(NUI\) soit un triangle isocèle en \(N\).
\(NUI\) est isocèle en \(N\) signifie que \(NU=NI\) ou que \(N\) est équidistant de \(U\) et de \(I\).
\(N\) est équidistant des extrémités de \([UI]\) donc \(N\) appartient à ... ?

Question 4

Construis un point \(C\) tel que \(LUCI\) soit un losange.
Un losange est un quadrilatère dont les 4 côtés ont la même longueur.
Donc tu dois construire \(C\) tel que \(CU=CI=UL=IL\).
Tu dois construire un point \(C\) tel que \(UC=IC=UL\) et tu dois le faire au compas.
Qu’est-ce qu’un losange ? Si tu ne sais plus revois le cours ou la vidéo sur les quadrilatères.
Un losange est un quadrilatère dont les 4 côtés ont la même longueur.
Tu dois donc construire un point \(C\) tel que \(CU=CI=LU=LI\).
Tu dois utiliser le compas.

Question 5

Démontre que le point \(C\) appartient à la droite \(d\).

On sait que \(LUCI\) est un losange donc, par définition, \(LU=UC=CI=IL\) et donc \(CU=CI\).

Ceci signifie que \(C\) est équidistant de \(U\) et de \(I\).

Or si un point est équidistant des extrémités d'un segment alors ce point appartient à la médiatrice de ce segment.

Donc \(C\) appartient à la médiatrice de \([UI]\).

Ce qui signifie que \(C\) appartient à la droite \(d\).

« Démontre que… » signifie que tu dois suivre les trois étapes :
On sait que… (données)
Or… (propriété)
Donc… (conclusion)


Que sais-tu sur le point \(C\) ?


\(LUCI\) est un losange donc \( CU=CI\).


Donc \(C\) est équidistant de \(U\) et de \(I\).