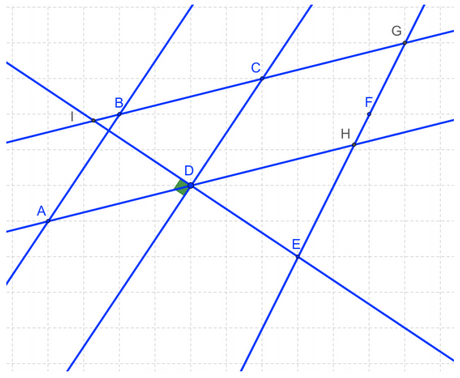
L'énoncé
Tu as obtenu le score de
Question 1
Coche la ou les bonnes réponses.
\(C \in (BG)\)
\(F \in (AD)\)
\(E \in [DI]\)
\(C\in [IB)\)
Connais-tu ce symbole : \(\in\) ?
Il signifie « appartient à ».
Attention à ne pas confondre droite, demi-droite et segment.
\(F \in (AD)\) est faux car \(A\), \(D\) et \(F\) ne sont pas alignés.
\(E \in [DI]\) est faux car \(E\) n’est pas situé entre \(I\) et \(D\).
Question 2
Coche la ou les bonnes réponses.
\((AB)//(BC)\)
\((AB)//(EF)\)
\((AB)//(ED)\)
\((AB)//(DC)\)
Tu peux imprimer la figure ou la recopier si besoin.
Compte les carreaux pour savoir si les droites sont parallèles.
On se déplace de \(A\) à \(B\) en faisant 2 carreaux à droites et 3 carreaux vers le haut. Le même chemin mène de \(D\) à \(C\) donc les droites \((AB)\) et \((DC)\) sont parallèles.
Question 3
Coche la ou les bonnes réponses.
\((BC)//(AD)\)
\((BG)//(HD)\)
\((CB)//(EF)\)
\((CB)\perp (DE)\)
Les questions 1 et 2 se ressemblent non ?
Ne confonds pas sécantes et perpendiculaires.
La droite \((BG)\) est la même que la droite \((BC)\).
\((CB)//(DA)\) est vraie car on se déplace de \(B\) à \(C\) en faisant 4 carreaux à droites et 1 carreau vers le haut. Le même chemin mène de \(A\) à \(D\) donc les droites sont parallèles.
La deuxième réponse est juste car il s’agit des mêmes droites.
Question 4
Coche la ou les bonnes réponses.
Le point d’intersection de \((AB)\) et \((EH)\) est \(G\).
Le point d’intersection de \((IB)\) et \((FH)\) est \(G\).
La parallèle à \((BC)\) passant par \(D\) coupe \((EF)\) en \(H\).
La parallèle à \((BC)\) passant par \(D\) coupe \((EH)\) en \( F\).
L’intersection de \((AB)\) et de \((EH)\) n’est pas sur la figure.
\((IB)\) et \((FH)\) se coupent en effet en \(H\).
Attention aux deux dernières phrases. L’intersection des deux droites est le point \(H\).
Question 5
Coche la ou les bonnes réponses.
\((IE)\perp (DC)\)
\((IE)\perp (AB)\)
La perpendiculaire à \((DC)\) passant par \(E\) coupe \((BC)\) en \(I\).
La perpendiculaire à \((DC)\) passant par \(E\) coupe \((IC)\) en \(B\).
Connais-tu bien le symbole de l’angle droit ?
N’oublie pas que \((AB)\) et \((CD)\) sont parallèles.
D’après la figure, \((IE)\) est perpendiculaire à \((DC)\). Comme \((AB)\) et \((DC)\) sont parallèles, alors \((IE)\) est aussi perpendiculaire à \((AB)\).
Attention aux deux dernières phrases. L’intersection des deux droites est le point \(I\).