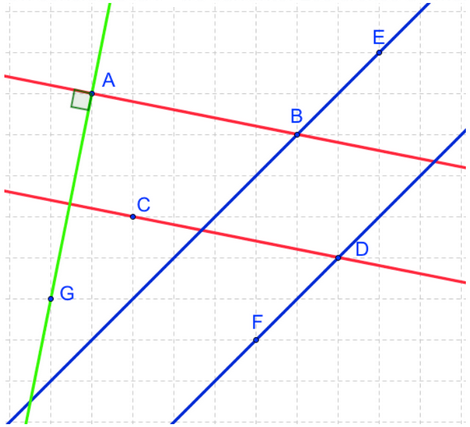
L'énoncé
Cet exercice est un QCM. Coche la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Pour se déplacer de \(A\) vers \(B\), on fait le trajet suivant :
5 carreaux à gauche, 1 carreau vers le bas.
5 carreaux à gauche, 1 carreau vers le haut.
5 carreaux à droite, 1 carreau vers le bas.
5 carreaux à droite, 1 carreau vers le haut.
On a bien dit de \(A\) vers \(B\).
Connais-tu bien ta droite ?
Tu peux remarquer que le déplacement qui permet d’aller de \(C\) à \(D\) est le même. C’est la raison pour laquelle les droites sont parallèles.
Question 2
Quel est le déplacement qui permet d'aller de \(E\) en \(B\) ou de \(D\) en \(F\) ?
2 carreaux à gauche, 2 carreaux en haut.
2 carreaux à droite, 2 carreaux en haut.
2 carreaux à gauche, 2 carreaux en bas.
2 carreaux à droite, 2 carreaux en bas.
Il suffit de compter les carreaux.
En allant de \(E\) vers \(B\).
Tu peux remarquer à nouveau que les droites \((EB)\) et \((DF)\) sont parallèles.
Question 3
Quel est le déplacement qui permet d'aller de \(G\) en \(C\) ? Que dire alors de \((EB)\) et \((CG)\) ?
2 carreaux à gauche, 2 carreaux en bas et \((EB)\) est sécante à \((CG)\).
\((CG)\) n’est pas tracée donc cette droite n’existe pas.
2 carreaux à droite, 2 carreaux en haut et \((EB)//(CG)\).
2 carreaux à gauche, 2 carreaux en bas et \((EB)//(CG)\).
Attention : on se déplace de \(G\) en \(C\) !
\((CG)\) n’est pas tracée mais tu peux le faire sur le papier ou mentalement. C’est toujours conseillé de compléter autant que tu veux une figure en géométrie.
Question 4
Coche la ou les bonnes réponses.
\((CB)//(AE)\)
\((CD) \perp (AG)\)
\((CF)\) et \((AD)\) sont sécantes.
\((CG)//(FD)\)
Tu peux reproduire ou imprimer la figure.
Tout se fait grâce aux carreaux.
Il suffit de comparer les déplacements.
Le trajet qui relie \(C\) à \(B\) (4 à droite et 2 en haut) n’est pas le même que celui qui relie \(A\) à \(E\) (7 à droite et 1 en haut).
Les droites ne sont donc pas parallèles.
On raisonne de la même façon pour les autre réponses.
Question 5
Coche la ou les bonnes réponses. La droite \((GC)\) non tracée est :
La perpendiculaire à \((GC)\) passant par \(C\).
La parallèle à \((DF)\) passant par \(C\).
La parallèle à \((BE) \) passant par \(G\).
La parallèle à \((BE)\) et \((FD)\).
Lis bien chaque phrase.
Combien y a-t-il de parallèles à \((BE)\) et \((FD)\) ?
\((GC)\) n’est bien sur pas perpendiculaire à elle-même.
Il y a une infinité de parallèles à \((BE)\) et \((FD)\) donc \((GC)\) n’est pas la seule.