L'énoncé
Exercice - Vecteurs et quadrilatères
Le plan est rapporté à un repère orthonormé \((O, I, J)\). On considère les points \(A(4 ; 4), B(7 ; 5)\) et \(C(8 ; 2)\).
Question 1
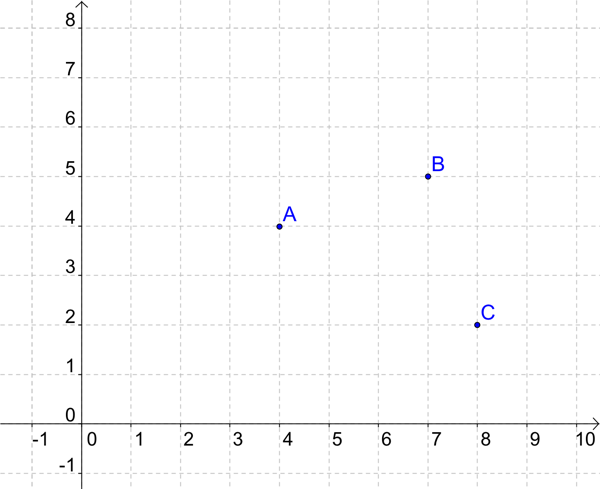
Placez les points \(A\), \(B\) et \(C\) sur une figure.
Aucune difficulté. C’est du programme de… 6ème !
Question 2
\(A(4 ; 4), B(7 ; 5)\) et \(C(8 ; 2)\).
Calculez les longueurs \(AB\), \(AC\) et \(BC\).
Longueur \(AB\) :
\(AB^2 = (x_B - x_A)^2 + (y_B - y_A)^2 \)
\(AB^2 = (7-4)^2 + (5-4)^2 \)
\(AB^2= 9+1 \)
\(AB^2= 10 \)
Longueur \(AC\) :
\(AC^2 = (x_C - x_A)^2 + (y_C - y_A)^2 \)
\(AC^2 = (8-4)^2 + (2-4)^2 \)
\(AC^2 = 16+4 \)
\(AC^2 = 20 \)
Longueur \(BC\) :
\(BC^2= (x_C - x_B)^2 + (y_C - y_B)^2 \)
\(BC^2= (8-7)^2 + (2-5)^2 \)
\(BC^2= 1+9 \)
\(BC^2= 10 \)
Ainsi :
\(AB = \sqrt{10}\)
\(AC = \sqrt{20} = 2\sqrt{5}\) et
\(BC = \sqrt{10}\) cm.
Lorsque vous calculez une longueur, vous pouvez dans un premier temps calculer son carré. Cela évite de recopier à chaque ligne une grande racine carrée.
Pensez à écrire les résultats sous la forme la plus simple possible.
Question 3
\(AB = \sqrt{10}\) cm, \(AC = \sqrt{20} = 2\sqrt{5}\) et \(BC = \sqrt{10}\) cm.
Démontrez que le triangle \(ABC\) est isocèle et rectangle.
On a : \(AC^2 = 20\) et
\(AB^2 + BC^2 = 10 + 10 = 20\).
Comme \(AC^2 = AB^2 + BC^2\), alors d'après la réciproque du théorème de Pythagore, \(ABC\) est un triangle rectangle en \(B\).
De plus, comme \(AB = BC\), alors \(ABC\) est isocèle en \(B\).
Le triangle \(ABC\) est donc rectangle et isocèle en \(B\).
Il sera facile de prouver que \(ABC\) est isocèle.
Pour prouver qu’il est rectangle, quelle propriété connaissez-vous ?
La réciproque de Pythagore bien sûr !
Question 4
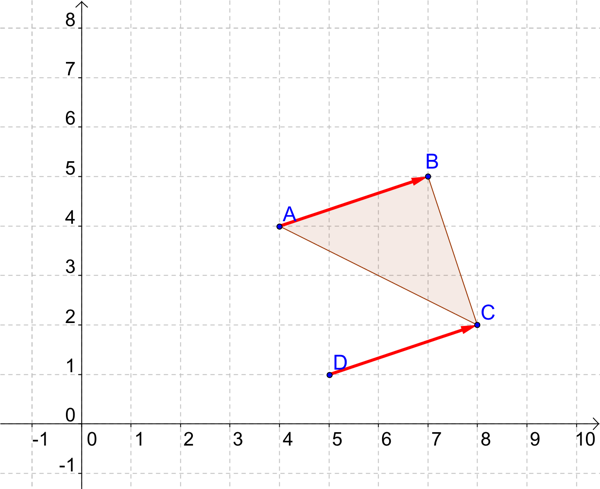
Placez, sur la figure, le point \(D\) tel que \(\overrightarrow{AB} = \overrightarrow{DC}\).
Savez-vous placer un point pour que deux vecteurs soient égaux ? Allez voir la vidéo dans les prérequis.
Cela signifie ici que \(ABCD\) est un parallélogramme.
Question 5
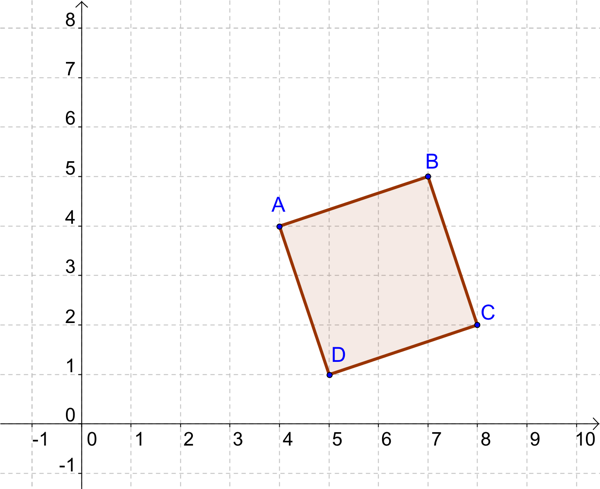
On sait que : \(\overrightarrow{AB} = \overrightarrow{DC}\) et que le triangle \(ABC\) est rectangle et isocèle en \(B\).
Quelle est la nature du quadrilatère \(ABCD\) ? Justifiez votre réponse.
Comme \(\overrightarrow{AB} = \overrightarrow{DC}\), alors \(ABCD\) est un parallélogramme.
De plus, comme \(ABC\) est un triangle rectangle \(B\), alors \(ABCD\) est un rectangle.
Comme \(ABC\) est isocèle en \(B\), alors \(ABCD\) est un carré.
Vous pouvez observer la figure pour avoir une idée de la réponse.
Cela ne prouve rien bien sûr. Cherchez des propriétés particulières de \(ABCD\).
Question 6
\(A(4 ; 4), B(7 ; 5)\) et \(C(8 ; 2)\)
Sachant que : \(\overrightarrow{AB} = \overrightarrow{DC}\), déterminez les coordonnées du point \(D(x_D;y_D)\).
On a : \(\overrightarrow{AB}(3 ; 1)\) et \(\overrightarrow{DC}(8 - x_D ; 2 - y_D) \)
Comme \(\overrightarrow{AB} = \overrightarrow{DC}\), alors :
\(8 - x_D = 3\) et \(2 - y_D = 1 \)
\(- x_D = 3 - 8\) et \(- y_D = 1 - 2 \)
\(x_D = 5\) et \(y_D = 1 \)
\(D\) a pour coordonnées \((5 ; 1)\).
Cherchez les coordonnées des deux vecteurs.
Comme les deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{DC}\) sont égaux alors ils ont les mêmes coordonnées.
Traduisez ceci par un système et le résoudre