Fiche de cours
Vecteurs et alignement
Méthodes :
Il existe plusieurs méthodes pour montrer que des points sont alignés. Par exemple, il est possible d'utiliser les coefficients directeurs de droites. Mais on peut aussi utiliser les vecteurs.
Pour rappel, deux points sont toujours alignés.
Méthode utilisant les vecteurs.
On se place dans un repère $(O; \overrightarrow{i}; \overrightarrow{j})$.
Soient $A(2; 1), B(-1: -5)$ et $C(10; 17)$ trois points du plan,
$A, B$ et $C$ sont-ils alignés ?
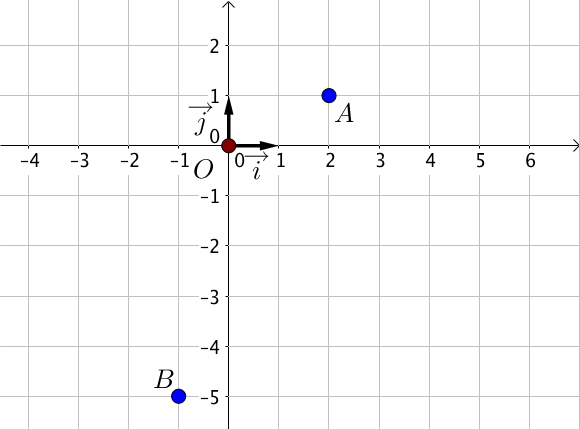
La méthode consiste à former deux vecteurs en utilisant les points dont on cherche à démontrer l'alignement en veillant à ce que ces deux vecteurs aient un point en commun.
Pour que les points soient alignés, il faudrait donc que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ par exemple soient colinéaires.
En effet, cela impliquerait que les droites $(AB)$ et $(AC)$ sont parallèles, avec un point en commun $A$ : les points $A, B$ et $C$ seraient ainsi alignés.
