Dans une entreprise travaillent 120 personnes ; il y a autant de femmes que d’hommes, $20\%$ des femmes parlent espagnol, $85\%$ des hommes ne parlent pas espagnol. On rentre une personne de cette entreprise. On désigne par $F$ « la personne est une femme », $H$ « la personne est un homme », $E$ « la personne parle espagnol »
1) Recopier et compléter le tableau d’effectif suivant.
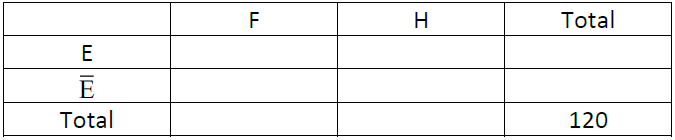
2) Déterminer les probabilités des événements suivant : $E$, $F \cap E$, $H \cap \overline{E}$ et $H \cup E$
3) On rencontre une personne de cette entreprise qui parle espagnol. Quelle est la probabilité pour que ce soit une femme ?
On désigne par $F$ « la personne est une femme », $H$ « la personne est un homme », $E$ « la personne parle espagnol ».
1) On complète le tableau d’effectifs :
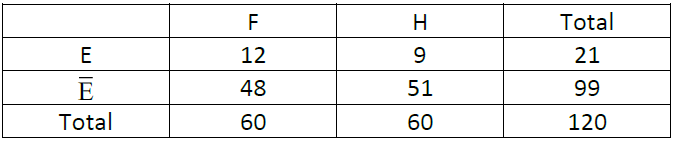
2) Déterminer les probabilités des événements suivant : $E$, $F \cap E$, $H \cap \overline{E}$ et $H \cup E$.
$P(E) = \dfrac{21}{120}$ ;
$P(F \cap E) = \dfrac{12}{120}$ ;
$P(H \cap \overline{E}) = \dfrac{51}{120}$ ;
$P(H \cup E) = \dfrac{12+9+51}{120} = \dfrac{72}{120}$.
3) On rencontre une personne de cette entreprise qui parle espagnol. Quelle est la probabilité pour que ce soit une femme ?
La réponse est $\dfrac{12}{21}$.
