L'énoncé
Exercice : Jeu de dés, probabililités et algorithmes
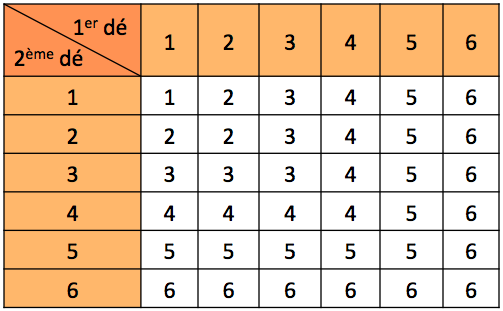
On lance deux dés cubiques équilibrés dont les faces sont numérotées de 1 à 6.
L’issue de l'expérience aléatoire est le maximum (autrement dit le plus grand) des deux numéros obtenus.
Par exemple, si les dés donnent 2 et 4, alors l’issue est 4.
Les probabilités seront données sous forme de fractions irréductibles.
Question 1
Question 2
Donner l'univers \(\Omega\) de cette expérience aléatoire.
\(\Omega = \{1 ; 2 ; 3 ; 4 ; 5 ; 6\}\)
L'univers d'une expérience aléatoire est l'ensemble de toutes les issues possibles ; chaque issue n'est répétée qu'une fois.
Question 3
Déterminer la loi de probabilité sur \(\Omega\).
- On cherche la probabilité d'obtenir 1.
- Sur les 36 résultats possibles, un seul donne 1 ; donc la probabilité d'obtenir 1 est de \(\frac{1}{36}\).
- On cherche la probabilité d'obtenir 2.
- Sur les 36 résultats possibles, trois donnent 2 ; donc la probabilité d'obtenir 2 est de \(\frac{3}{36}\).
- Et ainsi de suite pour 3 ; 4 ; 5 et 6. On obtient donc le tableau suivant :
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 |
| \(p_i\) | \(\dfrac{1}{36}\) | \(\dfrac{3}{36}\) | \(\dfrac{5}{36}\) | \(\dfrac{7}{36}\) | \(\dfrac{9}{36}\) | \(\dfrac{11}{36}\) |
Cela revient à donner la probabilité de chaque issue de \(\Omega\). On présente ce résultat sous forme de tableau.
Attention, il n'y a pas équiprobabilité ; on n'a pas autant de chance d'obtenir 1 que d'obtenir 6.
Combien comptez-vous de 1 ? Combien y a-t-il de résultats en tout ?
Et ainsi de suite pour les autres issues.
Question 4
On a :
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 |
| \(p_i\) | \(\dfrac{1}{36}\) | \(\dfrac{3}{36}\) | \(\dfrac{5}{36}\) | \(\dfrac{7}{36}\) | \(\dfrac{9}{36}\) | \(\dfrac{11}{36}\) |
Quelle est la probabilité de chacun des événements suivants ?
A : "Le maximum des deux numéros obtenus est égal à 6."
B : "Le maximum des deux numéros obtenus est inférieur ou égal à 4."
C : "Le maximum des deux numéros obtenus est impair."
Commençons par déterminer les ensembles A, B et C :
\(A = \{ 6 \}\)
\(B = \{ 1 ; 2 ; 3 ; 4 \}\)
\(C = \{ 1 ; 3 ; 5 \}\)
Calculons la probabilité de A :
\(p(A) = p(\{ 6 \})\) or, d'après la question 3 on sait que \(p({6}) = \dfrac{11}{36}\) donc \(p(A) = \dfrac{11}{36}\).
Calculons la probabilité de B :
\(p(B) = p(\{ 1 ; 2 ; 3 ; 4 \}\) soit \(p(B) = p(\{ 1 \}) + p(\{ 2 \})+ p(\{ 3 \})+ p(\{ 4 \})\)
\(p(B) = \dfrac{11}{36} + \dfrac{3}{36} + \dfrac{5}{36} + \dfrac{7}{36} \)
\(p(B) = \dfrac{16}{36}\) donc \(p(B) = \dfrac{4}{9}\)
Calculons la probabilité de C :
\(p(C) = p(\{ 1 ; 3 ; 5 \})\) soit \(p(C) = p(\{ 1 \}) + p(\{ 3 \})+ p(\{ 5 \})\)
\(p(C) = \dfrac{1}{36} + \dfrac{5}{36} + \dfrac{9}{36}\)
\(p(C) = \dfrac{15}{36}\) donc \(p(C) = \dfrac{5}{12}\)
Commencez par donner tous les éléments de A puis de B et de C.
La probabilité d'un événement est égale à la somme des probabilités des éléments élémentaires qui le constituent.
Pensez à donner les probabilités sous forme de fractions irréductibles.
Question 5
On donne les événements suivants :
A : "Le maximum des deux numéros obtenus est égal à 6."
B : "Le maximum des deux numéros obtenus est inférieur ou égal à 4."
Que dire des événements A et B ?
Les évènements A et B sont incompatibles car ils n'ont aucun élément en commun.
C'est en fait une question de cours ; on attend de vous que vous soyez capable de faire le lien avec une définition du cours.
Question 6
B : "Le maximum des deux numéros obtenus est inférieur ou égal à 4."
C : "Le maximum des deux numéros obtenus est impair."
Traduire par une phrase l'évènement \(B \cup C\) puis calculer sa probabilité.
D'après l'énoncé :
B : "Le maximum des deux numéros obtenus est inférieur ou égal à 4."
C : "Le maximum des deux numéros obtenus est impair."
Donc :
\(B \cup C\) : "Le maximum des deux numéros obtenus est impair OU inférieur ou égal à 4".
\(B \cup C = \{ 1 ; 3 ; 5 ; 2 ; 4 \}\)
Ainsi :
\(p(B \cup C) = p(\{ 1 ; 3 ; 5 ; 2 ; 4 \})\) soit
\(p(B \cup C) = p(\{ 1 \}) + p(\{ 2 \})+ p(\{ 3 \})+ p(\{ 4 \}) + p(\{ 5 \})\)
\(p(B \cup C) = \dfrac{1}{36} + \dfrac{3}{36}+ \dfrac{5}{36}+\dfrac{7}{36} +\dfrac{9}{36} \)
\(p(B \cup C) = \dfrac{25}{36}\)
Faites bien attention : \(\cup\) signifie "réunion" donc "OU".
Pour le calcul des probabilités, procèdez comme à la question 4 : donnez d'abord tous les éléments de \(B \cup C\) puis calculez la probabilité de \(B \cup C\).
Question 7
B : "Le maximum des deux numéros obtenus est inférieur ou égal à 4."
C : "Le maximum des deux numéros obtenus est impair."
Traduire par une phrase l'évènement \(B \cap \overline{C}\) puis calculer sa probabilité.
D'après l'énoncé :
B : "Le maximum des deux numéros obtenus est inférieur ou égal à 4."
\(\overline{C}\) : "Le maximum des deux numéros obtenus est pair."
Donc :
\(B \cap \overline{C}\) : "Le maximum des deux numéros obtenus est pair ET inférieur ou égal à 4."
\(B \cap \overline{C} = \{ 2 ; 4 \}\)
Ainsi :
\(p(B \cap \overline{C}) = p(\{ 2 ; 4 \})\) soit
\(p(B \cap \overline{C}) = p(\{ 2 \})+ p(\{ 4 \})\)
\(p(B \cup \overline{C}) = \dfrac{10}{36} \)
\(p(B \cup \overline{C}) = \dfrac{5}{1 8}\)
Faites bien attention : \(\cap\) signifie "intersection" donc "ET".
Quel est l'événement \(\overline{C}\) ?
Pour le calcul des probabilités procèdez comme à la question 4.
Question 8
On considère l'algorithme suivant :
Initialisation : S prend la valeur 0
Traitement : Pour \(i\) allant de 1 à 3
D \(\leftarrow\) 1+ENT(6*ALEA)
S prend la valeur S + D
Fin boucle pour
Sortie : Afficher S
En complétant le tableau de suivi ci-dessous, donner la valeur affichée par l'algorithme.
| Étape | Valeur prise par D | Valeur prise par S |
| Initialisation | / | |
| \(i=1\) | 4 | |
| \(i=2\) | 1 | |
| \(i=3\) | 6 |
| Étape | Valeur prise par D | Valeur prise par S |
| Initialisation | / | 0 |
| \(i=1\) | 4 | 4 |
| \(i=2\) | 1 | 5 |
| \(i=3\) | 6 | 11 |
Prenez votre temps !
1+ENT(6*ALEA) donne un nombre entier aléatoire entre 1 et 6.
Question 9
Que fait cet algorithme ? Quelle expérience aléatoire simule-t-il ?
D est un nombre aléatoire entre $1$ et $6$ ; donc D correspond au lancé d'un dé à $6$ faces.
S vaut d'abord 0 ; ensuite on ajoute dans S toutes les valeurs de D obtenues.
Par conséquent, cette expérience aléatoire simule le lancer de trois dés et affiche la somme des trois faces obtenues.
Prenez le temps de réfléchir aux nombres obtenus.
Que représente D ?
Que représente S ?