L'énoncé
Le plan est muni d'un repère orthonormal \((O, I, J)\).
L'unité est le centimètre.
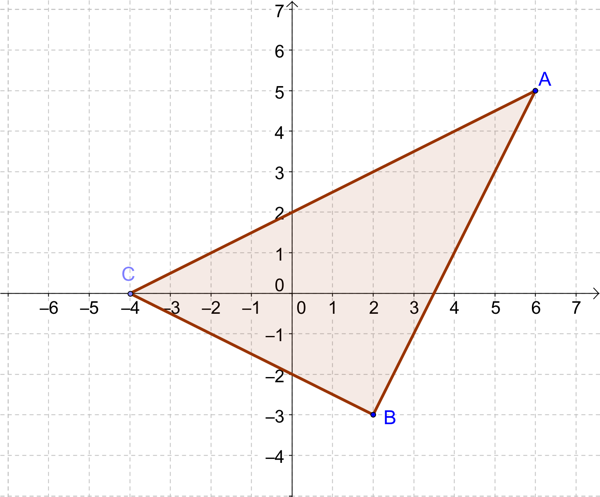
On considère les points \(A(6 ; 5), B(2 ; -3)\) et \(C(-4 ; 0)\).
Question 1
Placez les points \(A\), \(B\) et \(C\) sur une figure.
C’est du programme de 6ème…
Question 2
\(A(6 ; 5), B(2 ; -3)\) et \(C(-4 ; 0)\).
Calculez les distances \(AB\), \(BC\) et \(CA\) ;
Donnez les résultats sous la forme \(a\sqrt{5}\) où \(a\) est un nombre entier positif.
Distance \(AB\) :
\(AB^2 = (x_B - x_A)^2 + (y_B - y_A)^2 \)
\(AB^2 = (2-6)^2 + (-3 - 5)^2 \)
\(AB^2 = 16 + 64 \)
\(AB^2 = 80 \)
Distance \(AC\) :
\(AC^2 = (x_C - x_A)^2 + (y_C - y_A)^2 \)
\(AC^2 = (-4 - 6)^2 + (0 - 5)^2 \)
\(AC^2 = 100 + 25 \)
\(AC^2 = 125\)
Distance \(BC\) :
\(BC^2 = (x_C - x_B)^2 + (y_C - y_B)^2 \)
\(BC^2 = (-4 - 2)^2 + (0 - (-3)))^2 \)
\(BC^2 = 36 + 9 \)
\(BC^2 = 45 \)
Donc : \(AB = \sqrt{80} = 4\sqrt{5}\) cm,
\(AC = \sqrt{125} = 5\sqrt{5}\) cm et
\(BC = \sqrt{45} = 3\sqrt{5}\) cm.
Connaissez-vous bien la formule de la longueur d'un segment? Regardez la vidéo dans les prérequis.
Ici, on choisit de calculer le carré de la distance puis d’en prendre à la fin la racine carrée.
Question 3
On a : \(AB = \sqrt{80} = 4\sqrt{5}\) cm,
\(AC = \sqrt{125} = 5\sqrt{5}\) cm et
\(BC = \sqrt{45} = 3\sqrt{5}\) cm.
En déduire la nature du triangle \(ABC\). Justifiez votre réponse.
\(AB^2 + BC^2 = 80 + 45 = 125 \)
Comme \(AB^2 + BC^2 = AC^2\), alors d'après la réciproque du théorème de Pythagore, le triangle \(ABC\) est rectangle en \(B\).
Est-il isocèle, rectangle, équilatéral ?
Comme les trois longueurs sont différentes, il n’est ni isocèle ni équilatéral. Demandez vous donc s’il est rectangle.
Pour ce faire, utilisez la réciproque de Pythagore.
Question 4
\(AB = \sqrt{80} = 4\sqrt{5}\) cm,
\(AC = \sqrt{125} = 5\sqrt{5}\) cm et
\(BC = \sqrt{45} = 3\sqrt{5}\) cm.
Calculez l'aire du triangle \(ABC\).
Aire du triangle \(ABC\) :
\(A_{ABC} = \dfrac{AB \times BC}{2} = \dfrac{4\times 3\times 5}{2} = \dfrac{12 \times 5}{2} = 30\)
L'aire du triangle \(ABC\) vaut 30 cm\(^2\).
Connaissez-vous la formule de l’aire d’un triangle ?
\( Aire = \dfrac{(base \times hauteur)}{2}\)
Ici, comme le triangle est rectangle, on peut utiliser l’angle droit pour définir une base et une hauteur.
Question 5
\(AB = \sqrt{80} = 4\sqrt{5}\) cm,
\(AC = \sqrt{125} = 5\sqrt{5}\) cm et
\(BC = \sqrt{45} = 3\sqrt{5}\) cm.
Calculez le périmètre du triangle \(ABC\), donnez le résultat sous la forme \(a\sqrt{5}\), puis la valeur arrondie au dixième de ce résultat.
Périmètre du triangle \(ABC\) :
\(P = AB + BC + AC = (4 + 3 + 5)\times \sqrt{5}\ = 12\sqrt{5}\ \)
Le périmètre du triangle \(ABC\) est de \(12\sqrt{5}\) cm, soit environ 26,8 cm.
Savez-vous bien ce qu’est un périmètre ?
Il s’agit de la longueur du contour bien sûr.
Additionnez donc les longueurs des trois côtés !
Question 6
\(A(6 ; 5), B(2 ; -3)\) et \(C(-4 ; 0)\).
On considère le cercle circonscrit au triangle \(ABC\). Précisez la position de son centre \(E\) en justifiant la réponse. Calculez les coordonnées de ce point.
Comme le triangle \(ABC\) est rectangle en \(B\), alors ce triangle est inscrit dans un cercle qui a pour diamètre l'hypoténuse \([AC]\).
Le centre \(E\) du cercle circonscrit au triangle \(ABC\) est donc le milieu du segment \([AC]\).
Calculons ses coordonnées :
\(x_E = \dfrac{x_A+x_C}{2}\) et \(y_E = \dfrac{y_A+y_C}{2}\)
\(x_E = \dfrac{6+(-4)}{2}\) et \(y_E = \dfrac{5+0}{2}\)
\(x_E = \dfrac{2}{2}\) \(x_E = 1\) et \(y_E = \dfrac{5}{2}\)
Les coordonnées du point \(E\) sont : \((1 ; \dfrac{5}{2})\)
Connaissez-vous la particularité du centre du cercle circonscrit à un triangle rectangle ?
Il faut le savoir. Regardez la vidéo de rappel dans le cours de géométrie 3ème.
Connaissez-vous la formule des coordonnées du milieu d’un segment ? Regardez la vidéo dans le cours de géométrie plane de seconde.
Question 7
On a : \(E\) \((1 ; \dfrac{5}{2})\) et \(A(6 ; 5)\)
Déterminez la valeur exacte du rayon de ce cercle.
Ce cercle a pour rayon \(EA\). Calculons donc la distance \(EA\) :
\(EA^2 = (x_A - x_E)^2 + (y_A - y_E)^2\)
\(EA^2= (6 - 1)^2 + (5 - \dfrac{5}{2})^2\)
\(EA^2= 25 + \dfrac{25}{4}\)
\(EA^2= \dfrac{125}{4}\)
Donc : \(EA = \sqrt{\dfrac{125}{4}} = \dfrac{5\sqrt{5}}{2}\).
Le rayon du cercle est \(EA = \dfrac{5\sqrt{5}}{2}\) cm.
Observez bien la figure et cherchez un rayon ou un diamètre connu.
\(A\) est un point du cercle donc \(EA\) est un rayon.