L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
On se place dans un repère orthonormal.
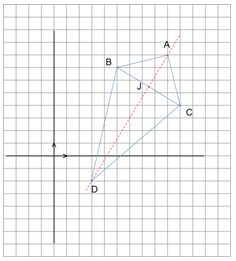
On considère les points suivants : \(A(9 ; 8), B(5 ; 7), C(10 ; 4), D(3 ;- 2)\). Soit \(J\) le milieu du segment \([BC]\).
Calculez les longueurs \(AB\) et \(AC\).
\(AB = \sqrt{17}\) et \(AC = \sqrt{17}\)
\(AB = \sqrt{5}\) et \(AC = \sqrt{17}\)
\(AB = \sqrt{17}\) et \(AC = \sqrt{5}\)
Aucune des trois réponses précédentes n’est exacte.
Besoin d’un rappel sur la formule de la distance entre deux points ?
\(AB = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2 )}\)
Vous pouvez aussi revoir ce résumé de cours. Allez voir la vidéo dans les prérequis.
On a :
\[AB = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2 }\] \[AB = \sqrt{(5-9)^2+(7-8)^2 }\] \[AB = \sqrt{(-4)^2+(-1)^2 }\] \[AB = \sqrt{16+1 }\] \[AB = \sqrt{17}\] Pour les mêmes raisons,
\[AC = \sqrt{17}\]
Question 2
Sachant que \(AB = \sqrt{17}\) et \(AC = \sqrt{17}\), le point \(A\) appartient-il à la médiatrice de \([BC]\) ?
Non.
Oui, car \(A\) est au milieu de \([BC]\).
Oui, car \(AB = AC\).
Aucune des trois réponses précédentes n’est exacte.
Savez-vous ce qu’est la médiatrice d’un segment ?
C’est la droite qui coupe perpendiculairement un segment en son milieu.
Savez-vous à quelle condition un point appartient à la médiatrice d’un segment ? Allez voir la vidéo dans les prérequis.
Le point \(A\) est à égale distance des extrémités du segment \([BC]\) donc il appartient à la médiatrice de ce segment.
Question 3
Le point \(D\) appartient-il à la médiatrice de \([BC]\) ?
Oui, car \(CD = BD = 85\).
Oui, car \(CD = BD = \sqrt{89}\).
Non.
Aucune des trois réponses précédentes n’est exacte.
C’est la même méthode que celle que vous venez d’utiliser.
On a :\[BD = \sqrt{(x_D-x_B)^2+(y_D-y_B)^2 }\] \[BD = \sqrt{(3-5)^2+(-2-7)^2 }\] \[BD = \sqrt{(-2)^2+(-9)^2 }\] \[BD = \sqrt{85 }\] Pour les mêmes raisons, \[BC = BD = \sqrt{85 }\] Le point \(D\) appartient bien à la médiatrice de \([BC]\) mais attention aux longueurs éronnés dans les propositions de réponses.
Question 4
On sait désormais que \(A\) et \(D\) appartiennent à la médiatrice de \([BC]\).
Que peut-on dire des points \(A\), \(D\) et \(J\) ?
Ils sont alignés.
\(I\) est le milieu de \([AD]\).
Ils ne sont pas alignés.
Aucune des trois réponses précédentes n’est exacte.
La médiatrice de \([BC]\) est donc la droite \((AD)\).
Le point \(I\) appartient-il à cette droite ?
\(J\) est le milieu de \([BC]\) et appartient donc à la médiatrice de ce segment
Il en est de même pour les points \(B\) et \(D\).
Ces trois points appartient donc à la médiatrice de \([BC]\)et sont donc alignés.
Question 5
Considérons à présent une nouvelle figure
Soit \((O ; I ; J)\) un repère orthonormal du plan. Soient les points \(A(6 ; 3)\) et \(B(8 ; - 3)\).
Soit \(H\) le pied de la hauteur du triangle \(ABJ\) issue du sommet \(A\) .
1. Démontrer que le triangle \(ABJ\) est isocèle.
\(ABJ\) est isocèle car \(AJ = AB = \sqrt{28}\).
\(ABJ\) est isocèle car \(AJ = AB = \sqrt{8}\).
\(ABJ\) est isocèle car \(AJ = AB = \sqrt{40}\).
Aucune des trois réponses précédentes n’est exacte.
Il vous suffit de calculer les longueurs \(AJ\) et \(AB\).
On a : \[AJ = \sqrt{(x_J-x_A)^2+(y_J-y_A)^2 }\] \[AJ = \sqrt{(0-6)^2+(1-3)^2 }\] \[AJ = \sqrt{40}\] Pour les mêmes raisons, on a : \[AJ =AB= \sqrt{40}\]
Question 6
On sait que : \(B(8 ; - 3)\).
Déterminez les coordonnées du point \(H\).
\(H\) a pour coordonnées \((0 ; - 1)\).
\(H\) a pour coordonnées \((8 ; - 2)\).
\(H\) a pour coordonnées \((4 ; - 1)\).
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous les propriétés des droites remarquables dans un triangle isocèle ?
En particulier, la hauteur issue de \(A\) est confondue avec la médiatrice de \([JB]\).
\(H\) est donc le milieu de… ?
Connaissez-vous la formule des coordonnées du milieu d’un segment ? Allez voir la vidéo.
Comme le triangle \(JAB\) est isocèle en \(A\), la hauteur issue de \(A\) est confondue avec la médiatrice de \([JB]\). Ainsi le point H est le milieu de \([JB]\)
On calcule donc les coordonnées du milieu de ce segment. Il vient : \[\left\{ \begin{array}{left} x_H = \frac{x_J+x_B}{2}\\ y_H = \frac{y_J+y_B}{2} \end{array}\right. \] \[\Leftrightarrow\left\{ \begin{array}{left} x_H = \frac{0+8}{2}\\ y_H = \frac{1+(-3)}{2} \end{array}\right. \] \[\Leftrightarrow\left\{ \begin{array}{left} x_H = 4\\ y_H = -1 \end{array}\right. \] Et finalement : \(H(4;-1)\)
Question 7
On change à nouveau de figure.
Soit le repère orthonormal \((O ; I ; J)\).
On considère les points \(A(8 ; 5), B(4 ; 2), C(4 ; - 3), D(8 ; 0)\).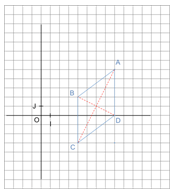 
On veut démontrer que le quadrilatère \(ABCD\) est un losange.
Pour cela, montrons dans un premier temps que \(ABCD\) est un parallélogramme.
Calculez les coordonnées des points \(K\) et \(L\), milieux respectifs de \([AC]\) et \([BD]\).
\(K(12 ; 2)\) et \(L(6 ; 1)\)
\(K(6 ; 1)\) et \(L(6 ; 1)\)
\(K(12 ; 2)\) et \(L(12 ; 2)\)
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous la formule des coordonnées du milieu d’un segment ?
Besoin d’un rappel ? Allez voir la vidéo.
Les coordonnées du milieu d'un segment sont données par la formule : \[\left\{ \begin{array}{left} x_K = \dfrac{x_A+x_C}{2}\\ y_K = \dfrac{y_A+y_C}{2} \end{array}\right. \] \[\Leftrightarrow\left\{ \begin{array}{left} x_K = \dfrac{8+4}{2}\\ y_K = \dfrac{5-3}{2} \end{array}\right. \] \[\Leftrightarrow\left\{ \begin{array}{left} x_K = 6\\ y_K = 1 \end{array}\right. \] Pour les mêmes raisons , on a : \(K(6 ; 1)\) et \(L(6 ; 1)\)
Question 8
On sait que : \(K(6 ; 1)\) et \(L(6 ; 1)\)
Cochez la bonne réponse :
\(ABCD\) est un parallélogramme car on sait que ses côtés opposés sont parallèles.
\(ABCD\) est un parallélogramme car on sait que ses côtés opposés ont la même longueur.
\(ABCD\) est un parallélogramme car ses diagonales ont le même milieu.
Aucune des trois réponses précédentes n’est exacte.
Attention à bien contrôler ce que vous savez (et dont vous êtes sur) et ce qui est sans doute vrai (mais que vous ne savez pas encore).
C'est une propriété caractéristique du parallélogramme. Si vous avez oublié, il y a des vidéos sur cette notion.
Question 9
\(A(8 ; 5), B(4 ; 2), C(4 ; - 3), D(8 ; 0)\).
On sait que \(ABCD\) est un parallélogramme. Calculez \(AB\) et \(AD\) et montrez finalement que \(ABCD\) est un losange.
\(AB = AD = 5\) donc \(ABCD\) est un losange car on sait qu’il a quatre côtés égaux.
\(AB = AD = 5\) donc \(ABCD\) est un losange car c’est un parallélogramme ayant deux côtés opposés de même longueur.
\(AB = AD = 5\) donc \(ABCD\) est un losange car c’est un parallélogramme ayant deux côtés consécutifs de même longueur.
Aucune des trois réponses précédentes n’est exacte.
Connaissez-vous les propriétés caractéristiques d’un losange ? Allez voir la vidéo.
On a : \[AD = \sqrt{(x_D-x_A)^2+(y_D-y_A)^2 }\] \[AD = \sqrt{(8-8)^2+(0-5)^2 } = 5\] On montre aussi facilement que \(AB =5\).
Ainsi :\(ABCD\) est un losange car c’est un parallélogramme ayant deux côtés consécutifs de même longueur.