Un petit muret $AN$ de $3$ mètres de hauteur est situé à $4$ mètres d’un mur $BM$. Au sol un projecteur mobile est dirigé sur ce muret et le mur derrière ; l’ombre du muret arrive en $M$ sur le mur.
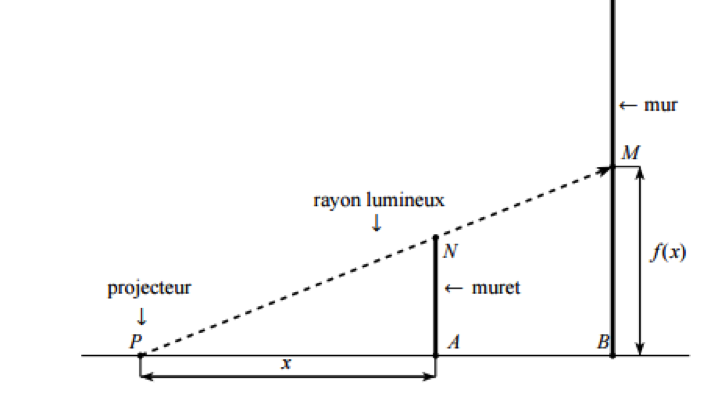
1) Montrer, en utilisant le théorème de Thalès, que $BM = 3 + \dfrac{12}{PA}$
2) Soit la fonction $f$ définie sur $ ]0; + \infty [$ par $f(x) = 3 + \dfrac{12}{x}$
Déterminer les variations de $f$ sur $]0; + \infty[$ puis dresser son tableau de variation.
3) Recopier puis compléter le tableau de valeurs suivant :
|
$x$ |
$0,5$ |
$1$ |
$3$ |
$6$ |
$15$ |
|
$f(x)$ |
|
|
|
|
|
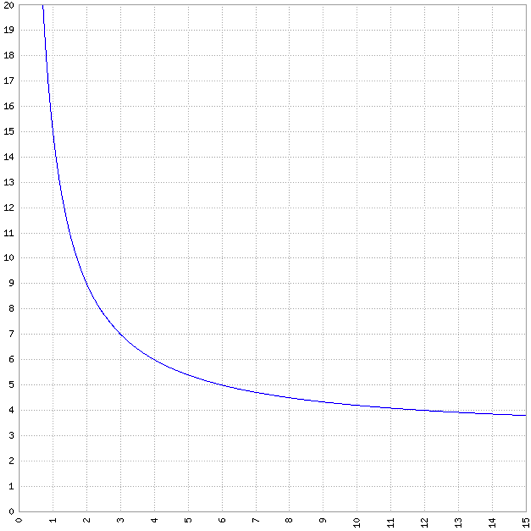
Représenter la fonction $f$ pour les valeurs de $x$ situées dans l’intervalle $]0; 15]$. On prendra comme unité le cm sur les deux axes.
1) Théorème de Thalès : $\dfrac{PA}{PB} = \dfrac{NA}{BM} = \dfrac{PN}{PM}$
$\dfrac{PA}{PB} = \dfrac{NA}{BM}$ On remplace avec les valeurs de l'énoncé $\dfrac{PA}{PA+4} = \dfrac{3}{BM}$
Par produit en croix, il vient $BM = 3 + \dfrac{12}{PA}$
2)

3)
|
$x$ |
$0,5$ |
$1$ |
$3$ |
$6$ |
$15$ |
|
$f(x)$ |
$27$ |
$15$ |
$7$ |
$5$ |
$3,8$ |