L'énoncé
Nous allons étudier la fonction \(f(x) = \dfrac{1}{x}\) définie sur \(\mathbb{R}^*\). On l’appelle aussi la fonction inverse.
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
\(f(x) = \dfrac{1}{x}\). Calculez l'image de $-3$.
\(f(-3) = \dfrac{1}{3}\)
\(f(-3) = -\dfrac{1}{3}\)
\(-3\)
Aucune des réponses précédentes n'est exacte.
\(f(-3)= \) ?
Remplacez \(x\) par -3 dans l'expression \(f(x) = \dfrac{1}{x}\).
Question 2
\(f(x) = \dfrac{1}{x}\). Calculez l'image de \(\dfrac{1}{2}\).
\(f\left(\dfrac{1}{2}\right) = -2 \)
\(f\left(\dfrac{1}{2}\right) =\dfrac{1}{2}\)
\(f\left(\dfrac{1}{2}\right) = 2 \)
Aucune des réponses précédentes n'est exacte.
C'est la même consigne que la question précédente.
Conservez l’écriture fractionnaire pour cette question.
\(f\left(\dfrac{1}{2}\right)= ? \)
Remplacez \(x\) par \(\dfrac{1}{2}\) dans l'expression \(f(x) = \dfrac{1}{x}\).
Question 3
Quelles sont les valeurs manquantes ? (dans l'ordre)
$\dfrac{1}{2};1;2;3;4;4;3;2;1;\dfrac{1}{2};\dfrac{1}{3}$
$\dfrac{1}{2};1;2;3;4;-4;-3;-2;-1;-\dfrac{1}{2};-\dfrac{1}{3}$
$-\dfrac{1}{2};-1;-2;-3;-4;4;3;2;1;\dfrac{1}{2};\dfrac{1}{3}$
Aucune des réponses précédentes n'est exacte.
Pour calculer l’inverse d’une fraction non nulle, il suffit d’inverser le numérateur et le dénominateur.
Attention la fonction inverse conserve le signe. Rien à voir avec l’opposé…
Question 4
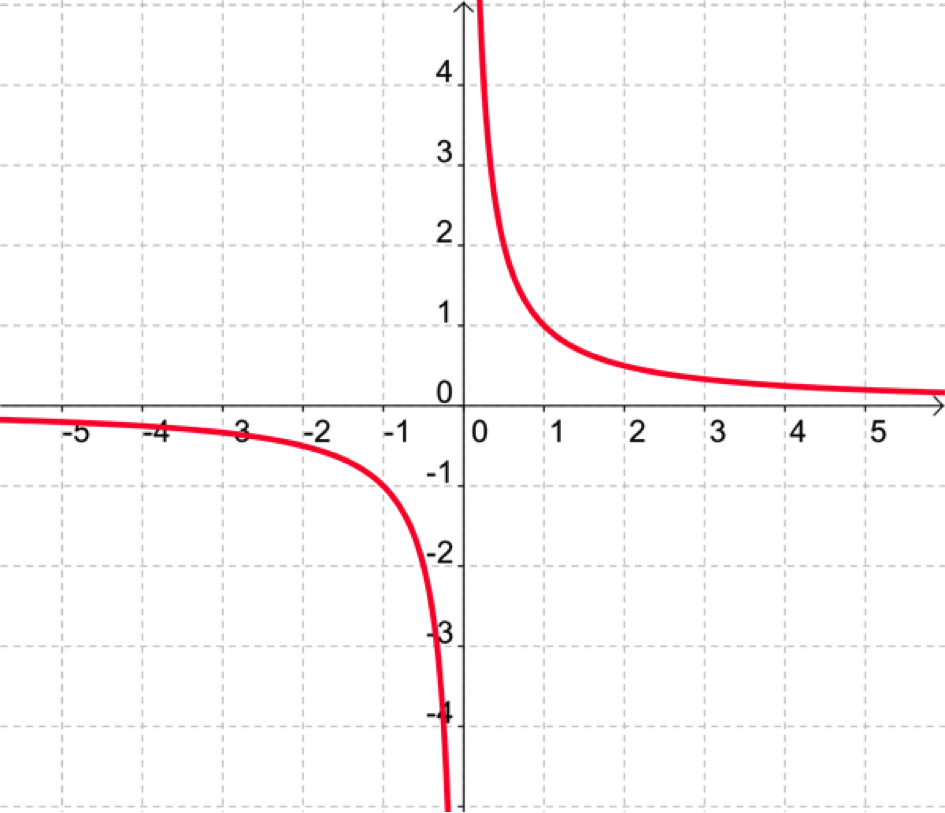
On a représenté les points dans un repère orthonormé et tracé la courbe représentant la fonction inverse.
Comment se nomme cette courbe ?
Une hyperbole
Une padebole
Une parabole
Aucune des réponses précédentes n’est exacte.
C’est du cours, pas de secret.
C’est un mot qu’on utilise en cours de français mais le sens n’est pas le même.
Votre professeur aurait pu le définir ainsi : Une ... consiste à mettre en relief une idée au moyen d’une expression exagérée.
Question 5
Sur cette courbe, lisez approximativement l'image de $-4$.
\(f(-4) \approx 0,25\)
\(f(-4) \approx -0,5\)
\(f(-4) \approx -4\)
Aucune des réponses précédentes n’est exacte.
Placez-vous au point d’abscisse -4 sur l’axe des abscisses.
Rejoignez la courbe.
Lisez la valeur sur l’axe des ordonnées.
Question 6
On va vérifier par le calcul.
Calculez \(f(-4)\).
\(f(-4) = -0,25\)
\(f(-4) = -0,5\)
\(f(-4) = -4\)
Aucune des réponses précédentes n’est exacte.
Vous devriez savoir faire à présent...
Remplacez le nombre \(x\) par -4 dans l’expression de \(f(x)\).
Question 7
Sur cette courbe, lisez à présent le ou les antécédents (s'ils existent) de 2.
L’antécédent vaut environ \(\dfrac{1}{2}\).
Les antécédents semblent être \(-\dfrac{1}{2}\) et \(\dfrac{1}{2}\).
2 n’a pas d’antécédent.
Aucune des réponses précédentes n’est exacte.
Placez-vous sur l’axe des ordonnées sur la 2ème graduation.
Tracez une droite horizontale passant par le point (0 ; 2).
Cette droite coupe la courbe. Pour quelles valeurs de \(x\) ?
Question 8
On va vérifier par le calcul.
Chercher les antécédents de $2$ revient à :
Chercher l’image de $2$.
Calculer \(f(2)\).
Résoudre \(f(x) = 2\).
Aucune des réponses précédentes n’est exacte.
C’est du cours. Chercher des antécédents revient à résoudre une équation.
Le nombre $2$ est l’image d’un nombre \(x\) que l’on ne connaît pas encore.
Question 9
Résolvons à présent \(f(x)=2\).
C'est à dire \( \dfrac{1}{x} = 2\).
L'ensemble des solutions est :
\(S = \{2\}\)
\(S = \{-\dfrac{1}{2}\}\)
\(S = \{\dfrac{1}{2}\}\)
Aucune des réponses précédentes n’est exacte.
Comme \(x\) n’est pas nul vous pouvez faire un produit en croix.
L’équation devient alors très simple. Vous avez abordé cette notion au collège
Ce n’est pas le moment de faire une erreur de signe.
Question 10
Vous connaissez l'antécédent de 2. Il s'agit du nombre \(\dfrac{1}{2}\).
Résolvez à présent l'inéquation : \(\dfrac{1}{x} \ge 2 \).
\(S = ]-\infty ; 0 [ \cup ]\dfrac{1}{2} ; +\infty[\)
\(S = ]0 ; \dfrac{1}{2} ]\)
\(S = \{0 ; \dfrac{1}{2} \}\)
Aucune des réponses précédentes n’est exacte.
Aidez-vous du graphique. Il faut que l’inverse des nombres cherchés soit supérieur à 2.
Quelle portion de courbe est concernée ?
À quelles valeurs de \(x\) cela correspond-il ?