L'énoncé
Nous allons étudier la fonction\(f(x) = \sqrt{x}\) définie sur \([0 ;+\infty [\).
On l’appelle aussi la fonction racine carrée.
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
\(f(x) = \sqrt{x}\). Calculez l'image de 16.
\(f(16) = 16\)
\(f(16) = \sqrt{4}\)
\(f(16) = 4\)
Aucune des réponses précédentes n’est exacte.
\(f(16) = ?\)
Remplacez \(x\) par 16 dans l’expression \(f(x) = \sqrt{x}\)
Question 2
\(f(x) = \sqrt{x}\). Calculez l'image de \(\dfrac{1}{4}\).
\(f\left(\dfrac{1}{4}\right) = \sqrt{\dfrac{1}{2}}\)
\(f\left(\dfrac{1}{4}\right) = \dfrac{1}{2}\)
\(f\left(\dfrac{1}{4}\right) = \dfrac{1}{\sqrt{2}}\)
Aucune des réponses précédentes n’est exacte.
C'est la même consigne que la question précédente.
Conservez l’écriture fractionnaire pour cette question.
La racine carrée d’un quotient est le quotient des racines.
Question 3
Quelles sont les valeurs manquantes ? (dans l'ordre)
$0;\dfrac{1}{25};1;2;\sqrt7;3;4;1000$
$0;\dfrac{1}{\sqrt5};1;2;\sqrt7;3;4;10$
$0;\dfrac{1}{5};1;2;\sqrt7;3;4;100$
Aucune des réponses précédentes n’est exacte.
Pour calculer la racine carrée d’un nombre, il suffit de se rappeler de la classe de 3ème.
Regardez les vidéos de 3ème sur ce chapitre. Un très bon professeur vous rappellera tout ce que vous avez oublié.
Attention à bien garder les valeurs exactes.
Question 4
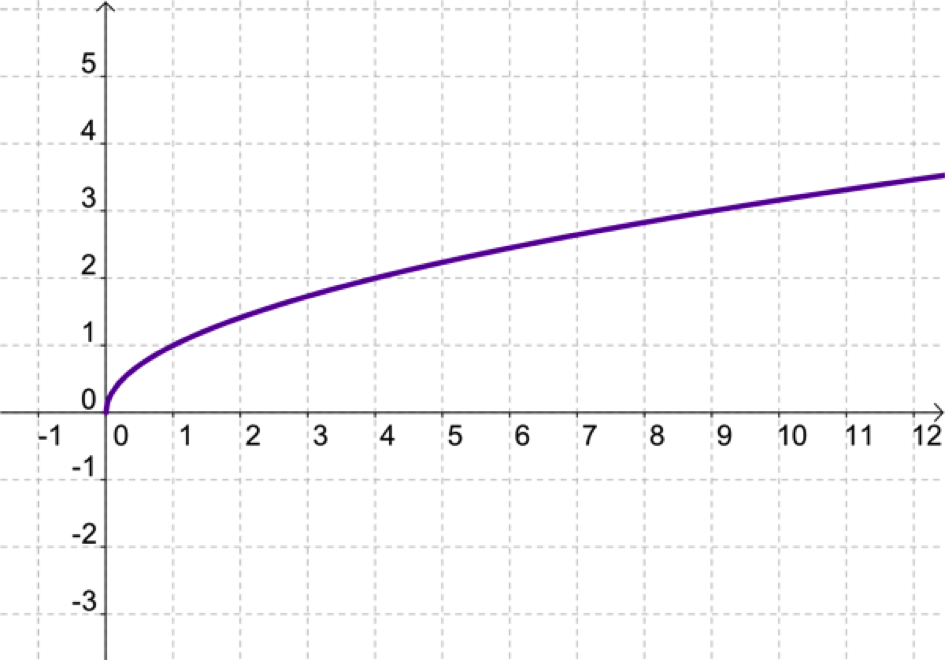
Voici la représentation graphique de la fonction racine carrée.
Quel est le lien entre cette courbe et la portion de parabole représentant la fonction \(f(x) = x^2\) pour les valeurs positives de \(x\)?
Ce sont les mêmes courbes.
Elles sont symétriques par rapport à la droite d’équation \(y = x\).
Elles sont symétriques par rapport à l’axe des ordonnées.
Aucune des réponses précédentes n’est exacte.
Tracez les deux courbes, ça devrait vous aider.
Il y a une belle symétrie on dirait.
Par rapport à quelle droite ?
Question 5
Sur cette courbe, lisez approximativement l'image de 9.
\(f(9) \approx 3\)
\(f(9) \approx 2,75\)
\(f(9) \approx 9\)
Aucune des réponses précédentes n’est exacte.
Partez de 9 sur l’axe des abscisses.
Rejognez la courbe.
Lisez la valeur sur l’axe des ordonnées.
Question 6
On va vérifier par le calcul.
Calculez \(f(9)\).
\(f(9) = 81\)
\(f(9) = 3\)
\(f(9) = -3\)
Aucune des réponses précédentes n’est exacte.
Vraiment besoin d'une astuce ? Vous devriez savoir faire à présent.
Remplacez le nombre \(x\) par 9 dans l’expression de \(f(x)\).
Cela ne devrait pas être trop dur de trouver la racine carrée de 9…
Question 7
Lisez à présent le ou les antécédents (s'ils existent) de 2.
L’antécédent de 2 vaut environ 4.
Les antécédents de 2 semblent être -4 et 4.
2 n’a pas d’antécédent.
Aucune des réponses précédentes n’est exacte.
Placez-vous sur l’axe des ordonnées sur la 2ème graduation.
Tracez une droite horizontale passant par le point (0 ; 2).
Cette droite coupe la courbe. Pour quelles valeurs de \(x\) ?
Question 8
On va vérifier par le calcul.
Chercher les antécédents de 2 revient à :
Chercher la racine carrée de 2.
Calculer \(f(2)\).
Résoudre \(f(x) = 2\).
Aucune des réponses précédentes n’est exacte.
C’est du cours. Chercher des antécédents revient à résoudre une équation.
Le nombre 2 est l’image d’un nombre \(x\) que l’on ne connaît pas encore.
Question 9
Résolvons à présent \(f(x) = 2\), c'est-à-dire \(\sqrt{x} = 2\).
L'ensemble des solutions est :
\(S=\{\sqrt{4}\}\)
\(S=\{\sqrt{2}\}\)
\(S=\{4\}\)
Aucune des réponses précédentes n’est exacte.
Comme ces deux nombres sont égaux, vous pouvez comparer leurs carrés.
Rappelez vous : Si \(a = b\) alors \(a^2 = b^2\).
La réponse devrait apparaître.
Question 10
Vous connaissez l'antécédent de 2. Il sagit du nombre 4.
Résolvez à présent l'inéquation : \(\sqrt{x} \le 2\).
\(S = [0 ; 4 ]\)
\(S = ]0;4]\)
\(S = \{0;4\}\)
Aucune des réponses précédentes n’est exacte.
Aidez-vous du graphique. Il faut que la racine carrée des nombres cherchés soit inférieure à 2.
Quelle portion de courbe est-elle concernée ?