L'énoncé
\(SABCD\) est une pyramide de sommet \(S\) ; la base \(ABCD\) est un parallélogramme.
\(M\) est un point de \([SC]\) et \(N\) un point de \([SB]\) ; de plus \((MN)\) est parallèle à \((BC)\).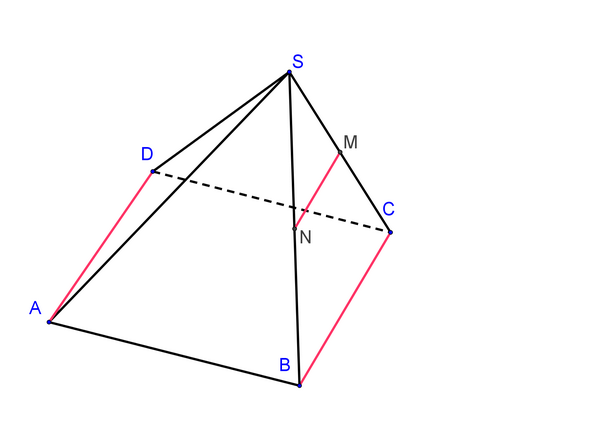
Question 1
Démontrez que les droites \((AD)\) et \((MN)\) sont parallèles.
\(ABCD\) est un parallélogramme donc ses côtés opposés sont parallèles.
On en déduit que \((BC) // (AD)\).
De plus, on sait d'après l'énoncé que \((BC) // (MN)\).
Si deux droites sont parallèles à une même troisième, elles sont parallèles entre elles.
Ainsi : \((AD) // (MN)\).
\(ABCD\) est un parallélogramme donc ses cotés opposés sont ?
Parallèles…
Question 2
Dans le plan \((ADMN)\), les droites \((AN)\) et \((DM)\) se coupent en un point noté \(P\).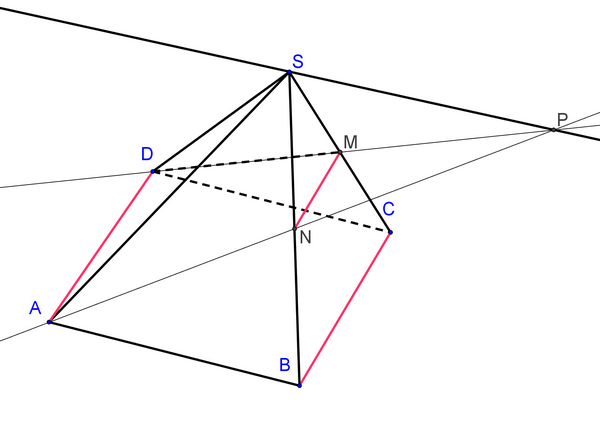 
Démontrez que le point \(P\) appartient au plan \((SAB)\).
Le point \(N\) appartient à \([SB]\) donc il appartient au plan \((SAB)\).
La droite \((AN)\) appartient elle aussi au plan \((SAB)\) donc chacun de ses points appartient aussi à ce plan.
C'est le cas de \(P\) qui est un point de la droite \((AN)\).
\(P\) appartient donc à \((SAB)\).
Et cette droite, dans quel plan est-elle située ?
Question 3
Montrez pour les mêmes raisons que \(P\) appartient au plan \((SDC)\).
Le point \(M\) appartient à \([SC]\) donc il appartient au plan \((SDC)\).
La droite \((DM)\) appartient elle aussi au plan \((SDC)\) donc chacun de ses points appartient aussi à ce plan.
C'est le cas de \(P\) qui est un point de la droite \((DM)\).
\(P\) appartient donc à \((SDC)\).
Une petite aide : le point \(P\) appartient à la droite \((DM)\).
Question 4
Pourquoi la droite d'intersection des plans \((SAB)\) et \((SDC)\) est-elle la droite \((SP)\) ?
\(S\) est un point appartenant à chaque plan donc il appartient à son intersection.
On sait d'après les deux questions précédentes que le point \(P\) appartient aussi à \((SAB)\) et \((SDC)\). On en déduit donc qu'il appartient à leur intersection.
L'intersection de deux plans sécants est une droite. On sait aussi que \(S\) et \(P\) sont deux points de cette intersection. Comme ils sont distincts, on en déduit que l'intersection des deux plans est la droite \((SP)\).
Il est évident que le point \(S\) est un point appartenant à chaque plan donc il appartient à son intersection.
Y a t-il un autre point vérifiant cela ?
Question 5
Déduisez-en que \((SP)\) est parallèle à \((AB)\) et à \((CD)\).
On sait que \(ABCD\) est un parallélogramme donc \((AB) // (CD)\).
Les plans \((SAB)\) et \((SDC)\) sont sécants et leur intersection est la droite \((SP)\).
Comme les droites \((AB)\) et \((CD)\) sont parallèles, alors, d'après le théorème du toit, on en conclut que \((SP)\) est aussi parallèle aux droites \((AB)\) et \((CD)\).
On va devoir utiliser un théorème qui met en scène deux plans sécants et deux parallèles…
Le théorème du toit. Un oubli ? Allez voir la vidéo dans les prérequis.