L'énoncé
On considère un cube \(ABCDEFGH\). Soit \(I\) le milieu de \([EF]\) et \(J\) celui de \([FG]\).
Question 1
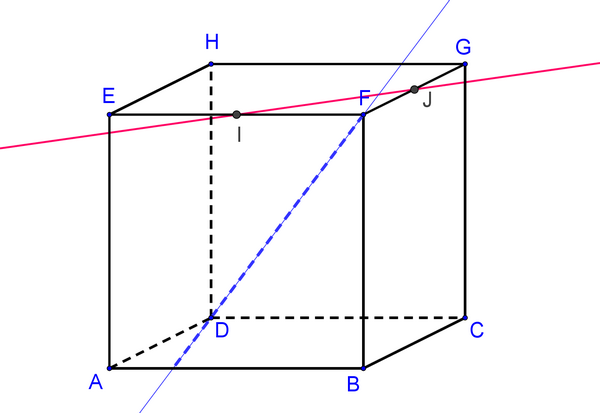
Les droites \((DF)\) et \((IJ)\) sont-elles coplanaires ?
La droite \((IJ)\) appartient au plan \((EFGH)\) car \(I\) et \(J\) sont les milieux de deux arêtes de ce plan.
La droite \((DF)\) est-elle dans ce plan ? Le point \(F\) est un point de ce plan mais le point \(D\) n'en est pas un. La droite \((DF)\) est donc sécante au plan \((EFGH)\). Comme \(F\) n'appartient pas à \((IJ)\), les droites ne sont pas coplanaires.
Pour que des droites soient coplanaires, il faut qu’elles soient sécantes ou parallèles.
Peut-on trouver un plan qui contient ces deux droites ?
Question 2
Représenter la droite d'intersection des plans \((ACH)\) et \((BDF)\).
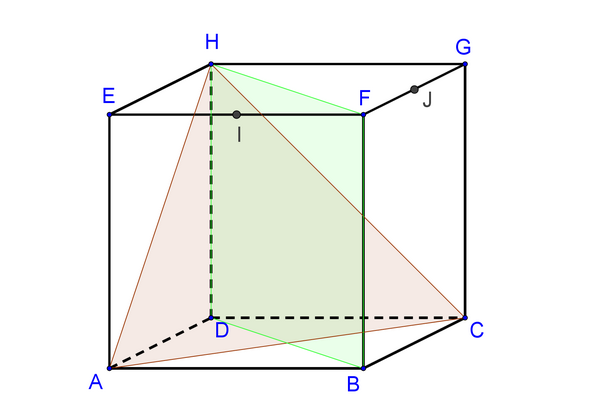
Le point \(H\) est un point du plan \((BFD)\) et c'est aussi un point de \((ACH)\).
Il appartient donc à l'intersection de ces deux plans.
Notons \(K\) l'intersection de \((AC)\) et de \((BD)\).
Le point \(K\) appartient à \((ACH)\) et aussi à \((BDF)\) donc il appartient à l'intersection de ces deux plans.
Finalement, comme \(H\) et \(K\) sont deux points distincts appartenant à l'intersection des deux plans \((BFD)\) et \((ACH)\), la droite \((HK)\) est l'intersection de ces deux plans.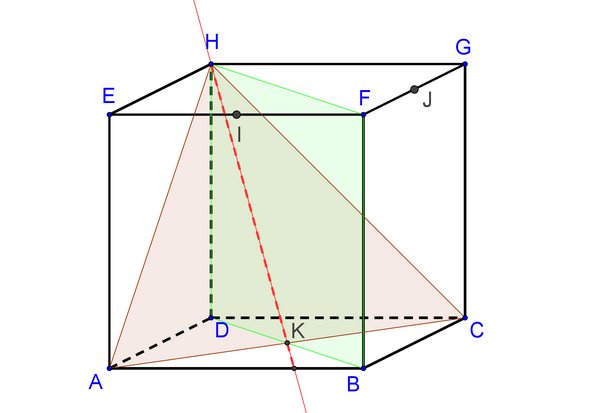
Il faut chercher deux points distincts de cette droite.
Que dire du point \(H\) ?
Le deuxième point n’est pas encore nommé. Cherchez le dans le plan \((ABCD)\).
Il s’agit de trouver un point commun aux droites \((AC)\) et \((BD)\). Nommez le \(K\).
Question 3
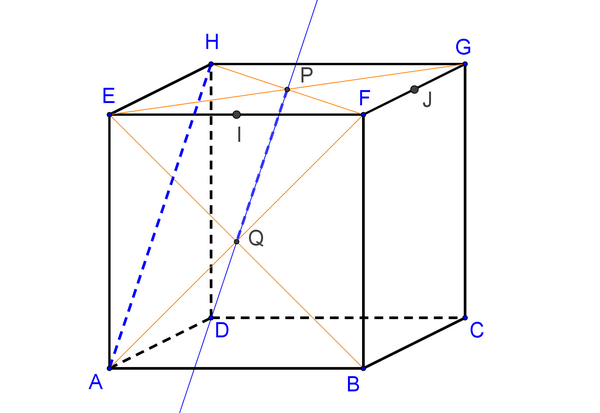
Soient \(P\) et \(Q\) les centres des carrés \(EFGH\) et \(ABFE\). Montrez que la droite \((PQ)\) est parallèle au plan \((ADHE)\).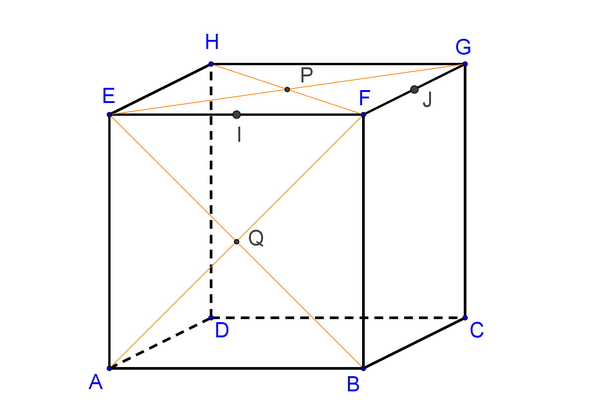
Dans le triangle \(HFA\), les points \(P\) et \(Q\) sont les milieux respectifs des côtés \([HF]\) et \([FA]\) car \(P\) et \(Q\) sont des centres de carrés donc situés au milieu des diagonales.
D'après la propriété de la droite des milieux, les droites \((QP)\) et \((HA)\) sont donc parallèles.
Or, la droite \((HA)\) est une droite du plan \((ADHE)\) donc la droite \((PQ)\) est parallèle à ce plan.
Vous pouvez alléger la figure en ne gardant que les informations essentielles
Cherchez une propriété dans le triangle \(HFA\).
Question 4
Quelle est l'intersection des plans \((PQH)\) et \((ADHE)\) ?
Le point \(F\) appartient à \((PH)\) donc il appartient au plan \((PQH)\).
Le point \(A\) appartient à la droite \((FQ)\) donc il appartient au plan \((PQH)\).
Les cinq points sont donc coplanaires et le plan \((PQH)\) est aussi le plan \((HFA)\).
Il apparaît que la droite \((HA)\) est une droite de ce plan ainsi qu'une droite du plan \((ADEH)\).
Conclusion, l'intersection des plans \((PQH)\) et \((ADEH)\) est la droite \((HA)\).
Cherchez d’autres points du plan \((PQH)\).
Le point \(F\) appartient à \((HP)\) donc ?
Du coup, que se passe t-il sur la droite \((QP)\) ?
Question 5
Montrez enfin que les plans \((BCGF)\) et \((PIQ)\) sont parallèles.
Dans le plan \((PIQ)\), les droites \((PI)\) et \((IQ)\) sont sécantes.
Dans le plan \((BCGF)\) les droites \((GF)\) et \((FB)\) sont sécantes.
Or, il se trouve que dans le carré \(ABFE\), les droites \((IQ)\) et \((FB)\) sont parallèles.
On sait aussi que dans le carré \(EFGH\), les droites \((PI)\) et \((GF)\) sont parallèles.
Dans l'espace, si deux droites sécantes d'un plan sont respectivement parallèles à deux autres droites sécantes d'un autre plan, alors, les deux plans sont parallèles.
Conclusion : les plans \((PIQ)\) et \((BCGF)\) sont parallèles.
Complétez la figure.
Connaissez-vous une condition pour prouver que deux plans sont parallèles ? Vous pouvez voir la vidéo dans les prérequis.