L'énoncé
\(ABC\) est un triangle quelconque. Le point \(P\) est défini par : \( \vec{AP}= \dfrac{1}{4} \vec{AB} \).
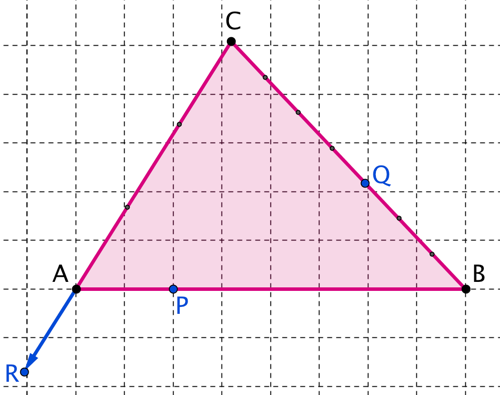
Les points \(R\) et \(Q\) sont disposés comme ci-dessous (on notera les graduations représentées par des points bleus) :
Question 1
Complète (par lecture graphique) les égalités suivantes :
\(\vec{AR}=
\text{........} \vec{AC} \)
\( \vec{BQ}=
\text{........} \vec{BC}\)
\(\vec{AR}= -\dfrac{1}{3} \vec{AC}\)
\(\vec{BQ}= \dfrac{3}{7} \vec{BC}\)
Aidez-vous des subdivisions : \([AC]\) est divisé en 3 donc…
Combien de subdivisions pour \([BC]\) ?
Question 2
Exprimer \(\vec{PR}\) en fonction de \(\vec{AB}\) et \(\vec{AC}\).
\(\vec{PR} = \vec{PA} + \vec{AR}\)
\( \vec{PR} = -\vec{AP} -\dfrac{1}{3} \vec{AC}\)
\( \vec{PR} =-\dfrac{1}{4} \vec{AB}-\dfrac{1}{3} \vec{AC}\)
La relation de Chasles bien sûr ! Et on introduit le point ?
Pour le savoir un petit coup d’œil sur l’égalité : \(\vec{AP}= \dfrac{1}{4} \vec{AB}\) et \( \vec{AR}= -\dfrac{1}{3} \vec{AC}\)
Le point qui apparaît dans ces formules est \( A\) : donc on démarre avec \( \vec{PR} = \vec{PA} + \vec{AR}\)
Question 3
Exprimer \( \vec{PQ}\) en fonction de \( \vec{AB}\) et \( \vec{AC}\).
\(\vec{PQ} = \vec{PA} + \vec{AQ}\)
\(\vec{PQ} = -\vec{AP} +\vec{AB}+\vec{BQ}\)
\(\vec{PQ} =-\dfrac{1}{4} \vec{AB} +\vec{AB}+\dfrac{3}{7} \vec{BC}\)
\(\vec{PQ} = \dfrac{3}{4} \vec{AB} + \dfrac{3}{7} \vec{BA}+\dfrac{3}{7} \vec{AC}\) (relation de Chasles sur \( \vec{BC})\)
\(\vec{PQ} = \dfrac{9}{28} \vec{AB} +\dfrac{3}{7} \vec{AC}\)
Et encore : \( \vec{AQ} = \vec{AB}+\vec{BQ}\) (on introduit \(B\) pour pouvoir utiliser que \( \vec{BQ}= \dfrac{3}{7} \vec{BC} \))
On remplace, on calcule… L’objectif étant de ne garder que les vecteurs \( \vec{AB}\) et \( \vec{AC}\).
Question 4
En déduire que \(\vec{PQ}\) et \( \vec{PR} \) sont colinéaires. Que peut-on en déduire ?
On a prouvé que :
\(\vec{PR} =- \dfrac{1}{4} \vec{AB} -\dfrac{1}{3} \vec{AC}\)
\(\vec{PQ} = \dfrac{9}{28}\vec{AB} +\dfrac{3}{7} \vec{AC}\)
Il faut aboutir à une relation du type : \(\vec{PQ} = k \vec{PR} \)
On a : \(\vec{PQ} = \dfrac{9}{28}\vec{AB} +\dfrac{3}{7} \vec{AC}\)
Factorisons par \( \dfrac{9}{7}\) :
\(\vec{PQ} =\dfrac{9}{7}\left( \dfrac{1}{4}\vec{AB} +\dfrac{1}{3} \vec{AC}\right)\)
\(\vec{PQ} =\dfrac{9}{7}\vec{PR} \)
Donc \(\vec{PQ}\) et \( \vec{PR}\) sont bien colinéaires. Cela montre que les points \( P, Q\) et \(R\) sont alignés.
Factorisez par \( \dfrac{9}{7}\)
Concluez.
Question 5
En se plaçant dans le repère \( (A; \vec{AB};\vec{AC} )\), montrer par une autre méthode qu'à la question 4) que les vecteurs \(\vec{PQ}\) et \(\vec{PR}\) sont colinéaires.
On sait que :
\(\vec{PR} =- \dfrac{1}{4} \vec{AB} - \dfrac{1}{3} \vec{AC}\)
\(\vec{PQ} = \dfrac{9}{28} \vec{AB} +\dfrac{3}{7} \vec{AC}\)
Cela permet de donner les coordonnées des vecteurs \(\vec{PQ} \) et \(\vec{PR}\) dans le repère \((A, \vec{AB},\vec{AC} )\) :
\(\vec{PR} \left(- \dfrac{1}{4}; - \dfrac{1}{3}\right)\)
\(\vec{PQ} \left(\dfrac{9}{28} ;\dfrac{3}{7} \right)\)
On applique le critère de colinéarité :
\(- \dfrac{1}{4}\times \dfrac{3}{7} = -\dfrac{3}{28}\)
\(-\dfrac{1}{3}\times \dfrac{9}{28} = -\dfrac{3}{28}\)
On obtient les mêmes résultats !
En conclusion, \( \vec{PQ}\) et \(\vec{PR} \) sont colinéaires (et les points \(P, Q\) et \(R \) sont alignés).
Celles de \(B\) sont : \(B(1;0)\)
Celles de \(C\) : \(C(0; 1)\)
