L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
La droite déquation cartésienne \(x-3y-9=0 \) passe par le point :
\(M(6 ;-1)\)
\(M(9 ;0)\)
\(M\left(\dfrac{1}{3} ;\dfrac{43}{15}\right)\)
\(M\left(\dfrac{3}{2} ;\dfrac{-5}{2}\right)\)
Remplacer les coordonnées dans l’équation de la droite pour voir si l'égalité est vérifiée.
Il suffit de remplacer par les coordonnées des point : facile… mais gare aux erreurs de calculs !
Question 2
La droite déquation cartésienne \(x-3y-9=0 \) a aussi pour équation :
\( \dfrac{1}{3}x-y-3=0\)
\(36y-12x+108=0\)
\(y= \dfrac{x}{3}-3\)
\(y= -\dfrac{3x}{5}+4\)
Par quel réel faut-il multiplier (ou diviser) l’équation d’origine pour obtenir celle proposée ?
Pour les équations réduites (soit \(y=mx+p\)), isoler le « \(y \)» pour se ramener à l’écriture \(y=mx+p\).
Tu dois savoir qu’une droite possède plusieurs équations cartésiennes (soit sous la forme \(ax+by+c=0\)), mais une seule équation réduite (sous la forme \(y=mx+p\)).
Attention, on peut multiplier tous les coefficients par un même nombre lorsque l’on a une équation cartésienne, mais pas lorsqu’il s‘agit d’une équation réduite (ainsi, la proposition 4 est fausse) !
Pour les propositions 2 : attention à l'ordre des termes.
La proposition 3 est aussi juste : on isole les y pour obtenir l’équation réduite :
\(\begin{align*}x-3y-9=0 &\Leftrightarrow -3y = -x+9\\ &\Leftrightarrow y= \dfrac{-x+9}{-3}\\ &\Leftrightarrow y= \dfrac{x}{3}-3\end{align*} \)
ou
\(\begin{align*}x-3y-9=0 &\Leftrightarrow -x+9=-3y \\ &\Leftrightarrow \dfrac{-x+9}{-3}= y\\ &\Leftrightarrow \dfrac{x}{3}-3 = y\end{align*}\)
Question 3
La droite déquation cartésienne \(x-3y-9=0 \) possède comme vecteur directeur :
\(\overrightarrow{u}\begin{pmatrix} 1 \\ -3 \end{pmatrix}\)
\(\overrightarrow{v}\begin{pmatrix} 3\\ 1 \end{pmatrix}\)
\(\overrightarrow{w}\begin{pmatrix} -3 \\ -1\end{pmatrix}\)
\(\overrightarrow{x}\begin{pmatrix} -7.5 \\ -2.5 \end{pmatrix}\)
Pour une équation de droite \(ax+by+c=0\) on peut prendre comme vecteur directeur : \(\overrightarrow{u}\begin{pmatrix} -b \\ a \end{pmatrix}\).
Pour trouver les autres vecteurs, il te suffit de voir s’ils sont colinéaires au vecteur directeur \(\overrightarrow{v}\begin{pmatrix} 3\\ 1 \end{pmatrix}\) (celui-ci étant obtenu par la formule de cours). Si nécessaire, utilises alors le critère de colinéarité (ou la proportionnalité des coordonnées) !
C’est une question très importante ! Uune droite possède une infinité de vecteurs directeurs (ils sont tous colinéaires entre eux) : une fois qu'on en a trouvé un, on les as tous ! Il suffit de prendre tous les vecteurs colinéaires à celui qu'on a trouvé. Par exemple ici, comme \(\overrightarrow{w}= -\overrightarrow{v}\) et \(\overrightarrow{x}= -2.5\overrightarrow{v}\) , on est sûr que c'est deux vecteurs sont bien des vecteurs directeurs de la droite.
Question 4
La droite cartésienne \(x-3y-9=0 \) est représentée par :
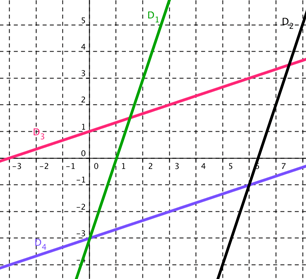
\(D_1\)
\(D_2\)
\(D_3\)
\(D_4\)
Quel est un vecteur directeur de la droite ?
\(\overrightarrow{v}\begin{pmatrix} 3 \\ 1\end{pmatrix}\)est un vecteur directeur (toujours la formule \(\overrightarrow{u}\begin{pmatrix} -b\\ a \end{pmatrix}\) ), cela te permet d’éliminer quelques candidates…
S'aider des points vérifiant l’équation de la droite (c’est la même équation que dans la question 1 : reprendre les points trouvés alors).
Calculer des coordonnées de points appartenant à la droite en utilisant l’équation donnée, puis comparer avec la figure. Mais un peu de vecteur directeur, ça change, non ?
Seules \(D_3\) et \(D_4\) admettent comme vecteur directeur le vecteur de coordonnées \(\overrightarrow{v}\begin{pmatrix} 3 \\ 1 \end{pmatrix}\). Et parmi ces droites, une seule passe par \(M(6 ;-1)\) : c’est \(D_4\) !
Question 5
On donne la représentation graphique dune droite \(D\) : 
Un vecteur directeur de \(D\) est \(\overrightarrow{u}\begin{pmatrix} 2 \\ -1\end{pmatrix}\)
Un vecteur directeur de \(D\) est \(\overrightarrow{v}\begin{pmatrix} -4 \\ 1\end{pmatrix}\)
Un vecteur directeur de \(D\) est \(\overrightarrow{w}\begin{pmatrix} 1 \\ -0.2\end{pmatrix}\)
Un vecteur directeur de \(D\) est \(\overrightarrow{x}\begin{pmatrix} 1 \\ -0.25\end{pmatrix}\)
Partir du point de coordonnées \((2 ;5)\) (ou \((-2 ;6)\)) pour lire un vecteur directeur : on rejoint la droite en se décalant horizontalement puis verticalement.
On lit comme coordonnées possibles d’un vecteur directeur \((4 ;-1)\) (ou \((-4 ;1)\) : ce sont deux vecteurs directeurs opposés).
Voir si les autres vecteurs proposés sont colinéaires à celui-ci.
Attention à ne pas se tromper dans le sens des déplacements lors des lectures graphiques.
Pour choisir entre les propositions 3 et 4, il ne faut pas utiliser le graphique (faire la différence entre \(0,2\) et \(0,25\) n’est pas facile sur le dessin), mais penser tester la colinéarité : on sait que \(\overrightarrow{v}\begin{pmatrix} -4 \\ 1\end{pmatrix}\) est un vecteur directeur de la droite, et \(\overrightarrow{x}= -\frac{1}{4}\overrightarrow{v} \) ou encore \(-4\overrightarrow{x} = \overrightarrow{v}\)
Ainsi, \(\overrightarrow{x}\) est bien un vecteur directeur !