L'énoncé
On a relevé les notes d’un devoir commun de mathématiques dans un lycée (Lycée A) dans une classe de terminale :
| Notes | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Effectifs | 2 | 1 | 1 | 2 | 6 | 9 | 9 | 11 | 8 | 8 | 8 | 4 | 6 | 3 | 4 |
Question 1
Déterminer la moyenne (arrondie à \(10^{-1}\)) et la médiane de cette série.
La moyenne est \(x =\dfrac { (3\times 2 + 4\times1 +5\times1 + 6\times2 + ... + 17\times 4)}{82}\approx10,8\) sur 20.
Comme \(N = 82\) est pair, on calcule \(\dfrac{N}{2}= 41\) et la médiane est la demi somme des valeurs de rang 41 et 42 :
La 41e note est 10 (additionne les effectifs au fur et à mesure).
La 42e est 11.
Donc \(M_e =\dfrac{(10+11)}{2} = 10,5\)
Trouver l’effectif total !
L’effectif total est 82 : utiliser la formule de la moyenne.
L’effectif total est 82 : est-il pair ou impair ? Utiliser la règle de calcul de la médiane.
Il faut prendre la valeur de rang 41 et de rang 42 et en faire la demi somme.
Question 2
Déterminer les quartiles de cette série.
On a \(N = 82\). Pour trouver les quartiles, on calcule \(\dfrac{N}{4}\) et \(\dfrac{3N}{4}\), puis on arrondit à lentier supérieur :
\(\dfrac{N}{4}=20,5\) et \(\dfrac{3N}{4}=60,5\)
Le premier quartile est la valeur de rang 21: \(Q_1=8\) (additionne les effectifs pour trouver la valeur de rang 21).
Le troisième quartile est la valeur de rang 61: \(Q_3=13 \).
Quel est l’effectif total ?
Ici, \(N = 82\). Pour trouver les quartiles, il faut trouver \(\dfrac{N}{4}\) et \(\dfrac{3N}{4}\).
Ne pas oublier d’arrondir à l’entier juste supérieur.
Question 3
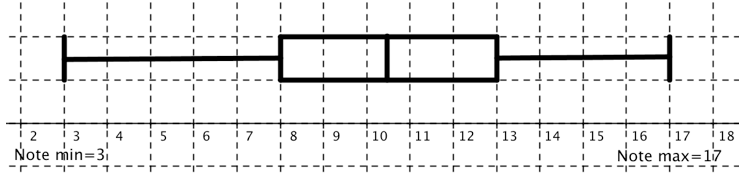
Construire le diagramme en boîte de cette série statistique
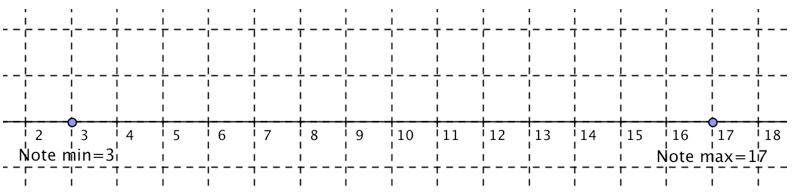
La première chose à faire de construire un axe gradué ou on fera figurer les notes.
Marquer ensuite l’emplacement de : la note minimale, la note maximale, \(M_e\), \(Q_1\) et \(Q_3\).
Juste au dessus de cet axe, dessiner le rectangle de bordure \(Q_1\) et \(Q_3\), puis les « moustaches ».
Question 4
Compléter les phrases :
La moitié des élèves ont une note supérieures à ... .
Environ ...% des élèves ont une note comprise entre 8 et 13.
La moitié des élèves ont une note supérieures à 10,5 (la médiane).
Environ 50% des élèves ont une note comprise entre 8 et 13 (intervalle interquartile).
A quel(s) indicateur(s) faut il penser lorsqu’on parle de la moitié de la population ?
Il est question de la médiane, ou de l’intervalle interquartile (qui contient la moitié de la population).
Les notes 8 et 13 sont des notes spéciales… (voir questions 1 et 2).
Question 5
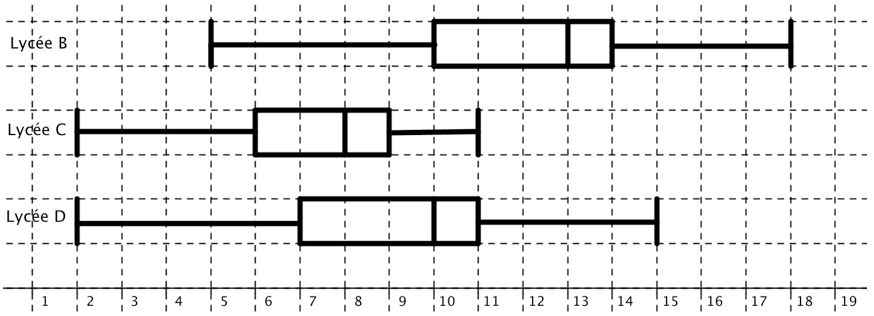
Le même devoir a été donné dans dautres établissements. On donne ci-dessous les diagrammes en boîte obtenus.
Répondre aux questions par lecture graphique :
a) Dans quel(s) lycée(s) un quart des élèves au moins a 11 ou plus ?
b) Dans quel(s) lycée(s) 25% au moins des élèves sont meilleurs que tous les élèves du lycée C ?
a) Dans le lycée D, puisque \(Q_3 = 11\).
Dans le lycée B car 50% des élèves ont même plus de 13 (médiane) : donc on peut dire quau moins 25% des élèves ont plus de 11 (c'est même un pourcentage bien plus élevé).
b) Dans les lycées D et B (la note maximale dans le lycée C est 11).
Bien lire le texte : il y a deux expressions importantes : un quart des élèves au moins (soit plus d’un quart) et ils doivent avoir 11 ou plus.
Revoir l’interprétation du diagramme en boîte donnée dans le cours !