Fiche de cours
Diagrammes en boîte et écart interquartile
Définition
Le diagramme en boîte est un schéma qui résume la série statistique.
Pour le construire, il faut avoir calculer au préalable la médiane et les quartiles.
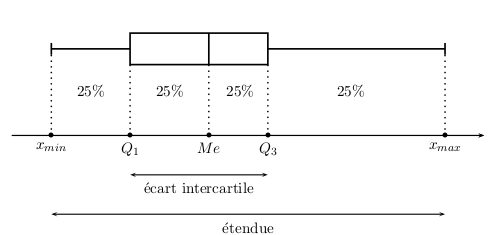
Les valeurs minimale et maximale de la série sont placées aux extrémités du diagramme.
Entre ces deux valeurs est placé un rectangle dont la première largeur correspond au premier quartile et la largeur opposée au troisième quartile.
Le segment contenu dans le rectangle correspond à la médiane.
L'écart interquartile correspond à la différence entre le troisième quartile et le premier, il est donc égal à $Q_3 - Q_1$.
L'intervalle interquartile est l'intervalle ayant pour bornes les quartiles, c'est à dire $[Q_1; Q_3]$. Il est visible sur le diagramme en boîte.
Exemple :
Considérons la série statistique suivante représentant les notes d'&
